Question Number 69873 by Masumsiddiqui399@gmail.com last updated on 28/Sep/19

Commented by mathmax by abdo last updated on 28/Sep/19
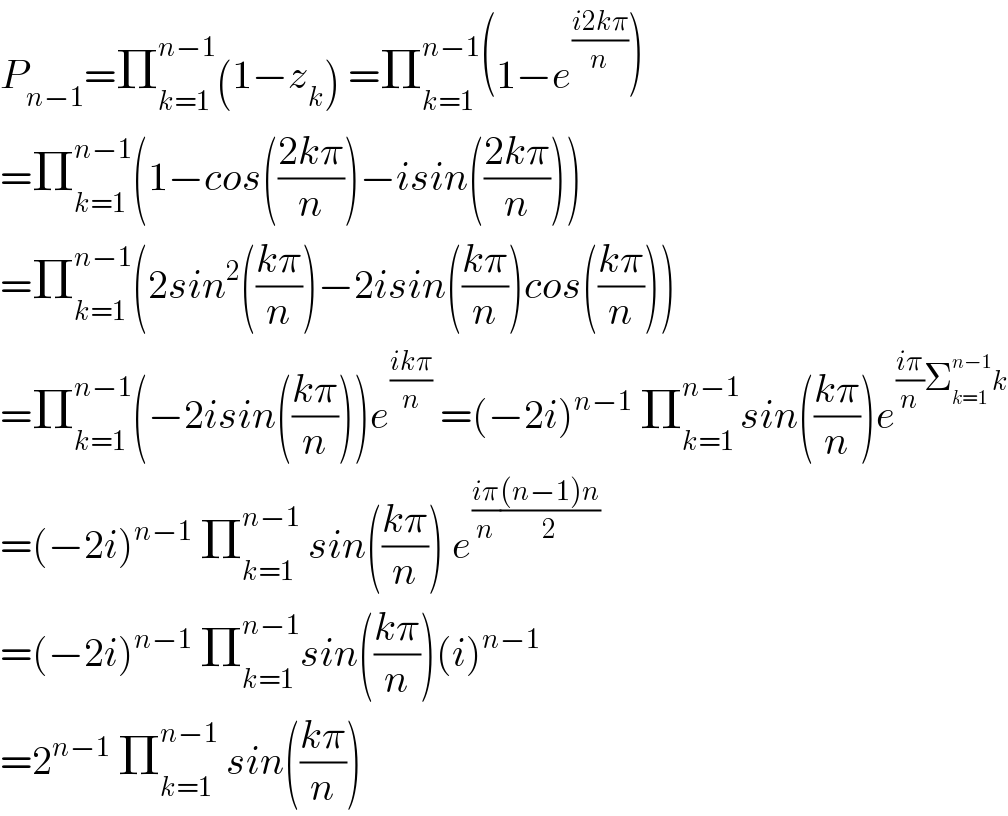
$${P}_{{n}−\mathrm{1}} =\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \left(\mathrm{1}−{z}_{{k}} \right)\:=\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \left(\mathrm{1}−{e}^{\frac{{i}\mathrm{2}{k}\pi}{{n}}} \right) \\ $$$$=\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \left(\mathrm{1}−{cos}\left(\frac{\mathrm{2}{k}\pi}{{n}}\right)−{isin}\left(\frac{\mathrm{2}{k}\pi}{{n}}\right)\right) \\ $$$$=\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \left(\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{k}\pi}{{n}}\right)−\mathrm{2}{isin}\left(\frac{{k}\pi}{{n}}\right){cos}\left(\frac{{k}\pi}{{n}}\right)\right) \\ $$$$=\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \left(−\mathrm{2}{isin}\left(\frac{{k}\pi}{{n}}\right)\right){e}^{\frac{{ik}\pi}{{n}}} \:=\left(−\mathrm{2}{i}\right)^{{n}−\mathrm{1}} \:\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} {sin}\left(\frac{{k}\pi}{{n}}\right){e}^{\frac{{i}\pi}{{n}}\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} {k}} \\ $$$$=\left(−\mathrm{2}{i}\right)^{{n}−\mathrm{1}} \:\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:{sin}\left(\frac{{k}\pi}{{n}}\right)\:{e}^{\frac{{i}\pi}{{n}}\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}} \\ $$$$=\left(−\mathrm{2}{i}\right)^{{n}−\mathrm{1}} \:\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} {sin}\left(\frac{{k}\pi}{{n}}\right)\left({i}\right)^{{n}−\mathrm{1}} \\ $$$$=\mathrm{2}^{{n}−\mathrm{1}} \:\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:{sin}\left(\frac{{k}\pi}{{n}}\right) \\ $$
