Question Number 70075 by ajfour last updated on 30/Sep/19
Commented by behi83417@gmail.com last updated on 30/Sep/19

Commented by behi83417@gmail.com last updated on 30/Sep/19
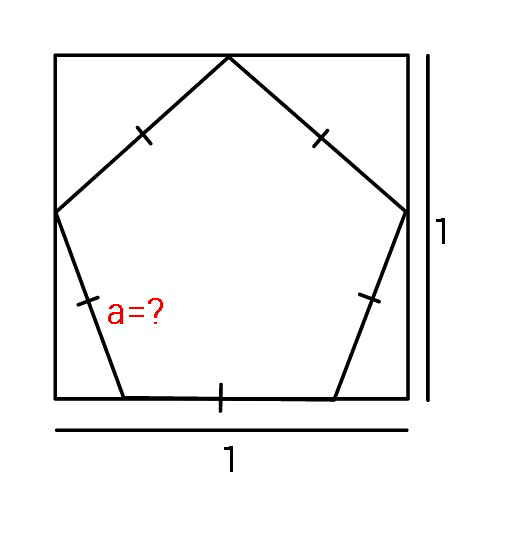
![∡ACB=((540)/5)=108^• AB^2 =a^2 +a^2 −2a^2 cos108^• AB^2 =BH^2 +1^2 ⇒2a^2 −2a^2 cos108−(a^2 /4)=1 ⇒7a^2 −8a^2 cos108=4 ⇒a^2 =(4/(7−8cos108^• ))⇒a=(2/( (√(7−8cos108^• )))) cos108^• =((1−(√5))/4) ⇒a=(2/( (√(7−8((1−(√5))/4)))))=(2/( (√(5+2(√5))))) .[=0.65]](https://www.tinkutara.com/question/Q70082.png)
$$\measuredangle\mathrm{ACB}=\frac{\mathrm{540}}{\mathrm{5}}=\mathrm{108}^{\bullet} \\ $$$$\mathrm{AB}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} −\mathrm{2a}^{\mathrm{2}} \mathrm{cos108}^{\bullet} \\ $$$$\mathrm{AB}^{\mathrm{2}} =\mathrm{BH}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2a}^{\mathrm{2}} −\mathrm{2a}^{\mathrm{2}} \mathrm{cos108}−\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{7a}^{\mathrm{2}} −\mathrm{8a}^{\mathrm{2}} \mathrm{cos108}=\mathrm{4} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{7}−\mathrm{8}\boldsymbol{\mathrm{cos}}\mathrm{108}^{\bullet} }\Rightarrow\mathrm{a}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{7}−\mathrm{8cos108}^{\bullet} }} \\ $$$$\mathrm{cos108}^{\bullet} =\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{a}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{7}−\mathrm{8}\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}}}\:\:.\left[=\mathrm{0}.\mathrm{65}\right] \\ $$
Commented by ajfour last updated on 01/Oct/19
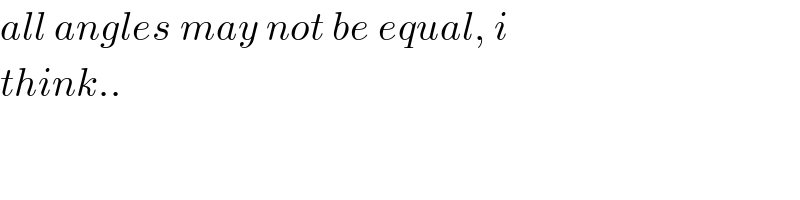
$${all}\:{angles}\:{may}\:{not}\:{be}\:{equal},\:{i} \\ $$$${think}.. \\ $$
