Question Number 70108 by naka3546 last updated on 01/Oct/19
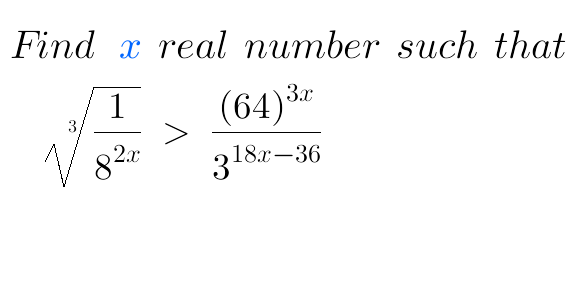
Answered by MJS last updated on 01/Oct/19

$$\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{x}} >\mathrm{3}^{\mathrm{36}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{18}{x}} \\ $$$$\left(−\mathrm{2ln}\:\mathrm{2}\right){x}>\mathrm{36ln}\:\mathrm{3}\:+\mathrm{18}\left(\mathrm{ln}\:\mathrm{2}\:−\mathrm{ln}\:\mathrm{3}\right){x} \\ $$$$\left(\mathrm{18ln}\:\mathrm{3}\:−\mathrm{20}\:\mathrm{ln}\:\mathrm{2}\right){x}>\mathrm{36ln}\:\mathrm{3} \\ $$$${x}>\frac{\mathrm{18ln}\:\mathrm{3}}{\mathrm{9ln}\:\mathrm{3}\:−\mathrm{10ln}\:\mathrm{2}}\approx\mathrm{6}.\mathrm{68970287} \\ $$
