Question Number 70121 by ahmadshahhimat775@gmail.com last updated on 01/Oct/19
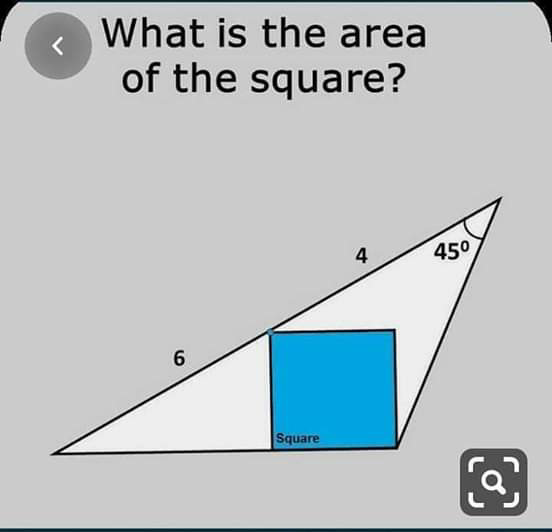
Answered by mind is power last updated on 01/Oct/19
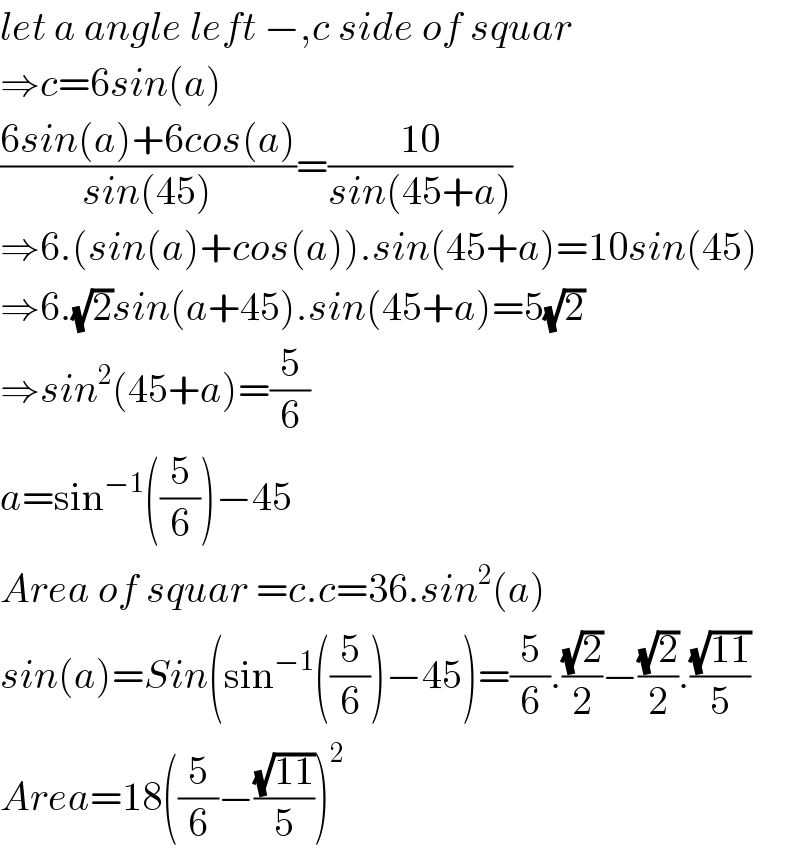
$${let}\:{a}\:{angle}\:{left}\:−,{c}\:{side}\:{of}\:{squar} \\ $$$$\Rightarrow{c}=\mathrm{6}{sin}\left({a}\right) \\ $$$$\frac{\mathrm{6}{sin}\left({a}\right)+\mathrm{6}{cos}\left({a}\right)}{{sin}\left(\mathrm{45}\right)}=\frac{\mathrm{10}}{{sin}\left(\mathrm{45}+{a}\right)} \\ $$$$\Rightarrow\mathrm{6}.\left({sin}\left({a}\right)+{cos}\left({a}\right)\right).{sin}\left(\mathrm{45}+{a}\right)=\mathrm{10}{sin}\left(\mathrm{45}\right) \\ $$$$\Rightarrow\mathrm{6}.\sqrt{\mathrm{2}}{sin}\left({a}+\mathrm{45}\right).{sin}\left(\mathrm{45}+{a}\right)=\mathrm{5}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{sin}^{\mathrm{2}} \left(\mathrm{45}+{a}\right)=\frac{\mathrm{5}}{\mathrm{6}} \\ $$$${a}=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{6}}\right)−\mathrm{45} \\ $$$${Area}\:{of}\:{squar}\:={c}.{c}=\mathrm{36}.{sin}^{\mathrm{2}} \left({a}\right) \\ $$$${sin}\left({a}\right)={Sin}\left(\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{6}}\right)−\mathrm{45}\right)=\frac{\mathrm{5}}{\mathrm{6}}.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}.\frac{\sqrt{\mathrm{11}}}{\mathrm{5}} \\ $$$${Area}=\mathrm{18}\left(\frac{\mathrm{5}}{\mathrm{6}}−\frac{\sqrt{\mathrm{11}}}{\mathrm{5}}\right)^{\mathrm{2}} \\ $$
