Question Number 70159 by ajfour last updated on 01/Oct/19

Commented by ajfour last updated on 01/Oct/19

$${Under}\:{balanced}\:{conditions},\:{find} \\ $$$$\theta\:.\:{All}\:{surfaces}\:{frictionless}. \\ $$
Answered by mr W last updated on 01/Oct/19

Commented by mr W last updated on 01/Oct/19
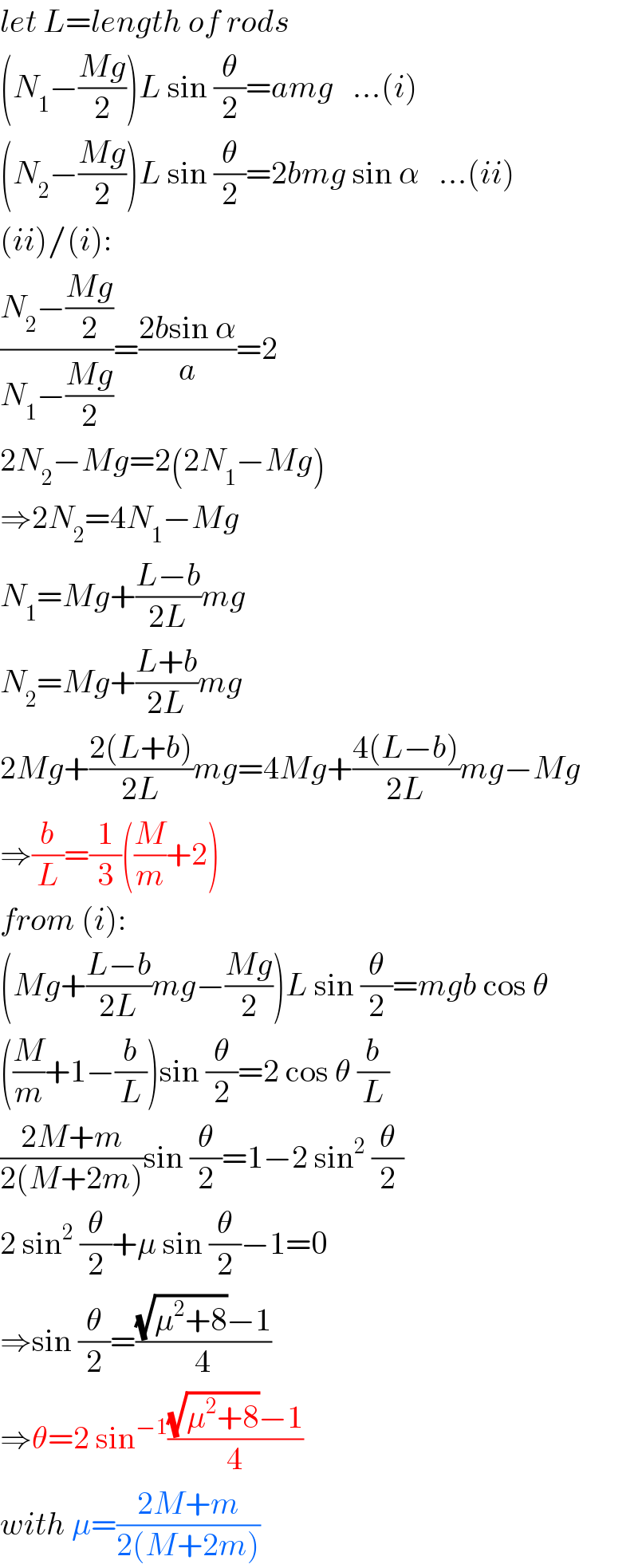
$${let}\:{L}={length}\:{of}\:{rods} \\ $$$$\left({N}_{\mathrm{1}} −\frac{{Mg}}{\mathrm{2}}\right){L}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}={amg}\:\:\:…\left({i}\right) \\ $$$$\left({N}_{\mathrm{2}} −\frac{{Mg}}{\mathrm{2}}\right){L}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\mathrm{2}{bmg}\:\mathrm{sin}\:\alpha\:\:\:…\left({ii}\right) \\ $$$$\left({ii}\right)/\left({i}\right): \\ $$$$\frac{{N}_{\mathrm{2}} −\frac{{Mg}}{\mathrm{2}}}{{N}_{\mathrm{1}} −\frac{{Mg}}{\mathrm{2}}}=\frac{\mathrm{2}{b}\mathrm{sin}\:\alpha}{{a}}=\mathrm{2} \\ $$$$\mathrm{2}{N}_{\mathrm{2}} −{Mg}=\mathrm{2}\left(\mathrm{2}{N}_{\mathrm{1}} −{Mg}\right) \\ $$$$\Rightarrow\mathrm{2}{N}_{\mathrm{2}} =\mathrm{4}{N}_{\mathrm{1}} −{Mg} \\ $$$${N}_{\mathrm{1}} ={Mg}+\frac{{L}−{b}}{\mathrm{2}{L}}{mg} \\ $$$${N}_{\mathrm{2}} ={Mg}+\frac{{L}+{b}}{\mathrm{2}{L}}{mg} \\ $$$$\mathrm{2}{Mg}+\frac{\mathrm{2}\left({L}+{b}\right)}{\mathrm{2}{L}}{mg}=\mathrm{4}{Mg}+\frac{\mathrm{4}\left({L}−{b}\right)}{\mathrm{2}{L}}{mg}−{Mg} \\ $$$$\Rightarrow\frac{{b}}{{L}}=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{M}}{{m}}+\mathrm{2}\right) \\ $$$${from}\:\left({i}\right): \\ $$$$\left({Mg}+\frac{{L}−{b}}{\mathrm{2}{L}}{mg}−\frac{{Mg}}{\mathrm{2}}\right){L}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}={mgb}\:\mathrm{cos}\:\theta \\ $$$$\left(\frac{{M}}{{m}}+\mathrm{1}−\frac{{b}}{{L}}\right)\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\mathrm{2}\:\mathrm{cos}\:\theta\:\frac{{b}}{{L}} \\ $$$$\frac{\mathrm{2}{M}+{m}}{\mathrm{2}\left({M}+\mathrm{2}{m}\right)}\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}\: \\ $$$$\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}+\mu\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{\sqrt{\mu^{\mathrm{2}} +\mathrm{8}}−\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\theta=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mu^{\mathrm{2}} +\mathrm{8}}−\mathrm{1}}{\mathrm{4}} \\ $$$${with}\:\mu=\frac{\mathrm{2}{M}+{m}}{\mathrm{2}\left({M}+\mathrm{2}{m}\right)} \\ $$
Commented by ajfour last updated on 01/Oct/19

$${looks}\:{right}\:{sir},\:{let}\:{me}\:{check} \\ $$$${in}\:{detail}\:{in}\:{some}\:{while},\:{thanks}! \\ $$
Commented by ajfour last updated on 02/Oct/19
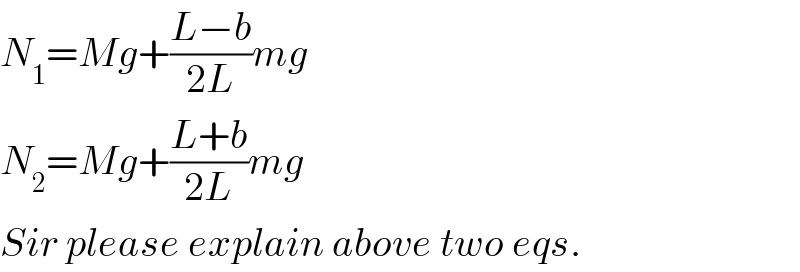
$${N}_{\mathrm{1}} ={Mg}+\frac{{L}−{b}}{\mathrm{2}{L}}{mg} \\ $$$${N}_{\mathrm{2}} ={Mg}+\frac{{L}+{b}}{\mathrm{2}{L}}{mg} \\ $$$${Sir}\:{please}\:{explain}\:{above}\:{two}\:{eqs}. \\ $$
Commented by mr W last updated on 02/Oct/19
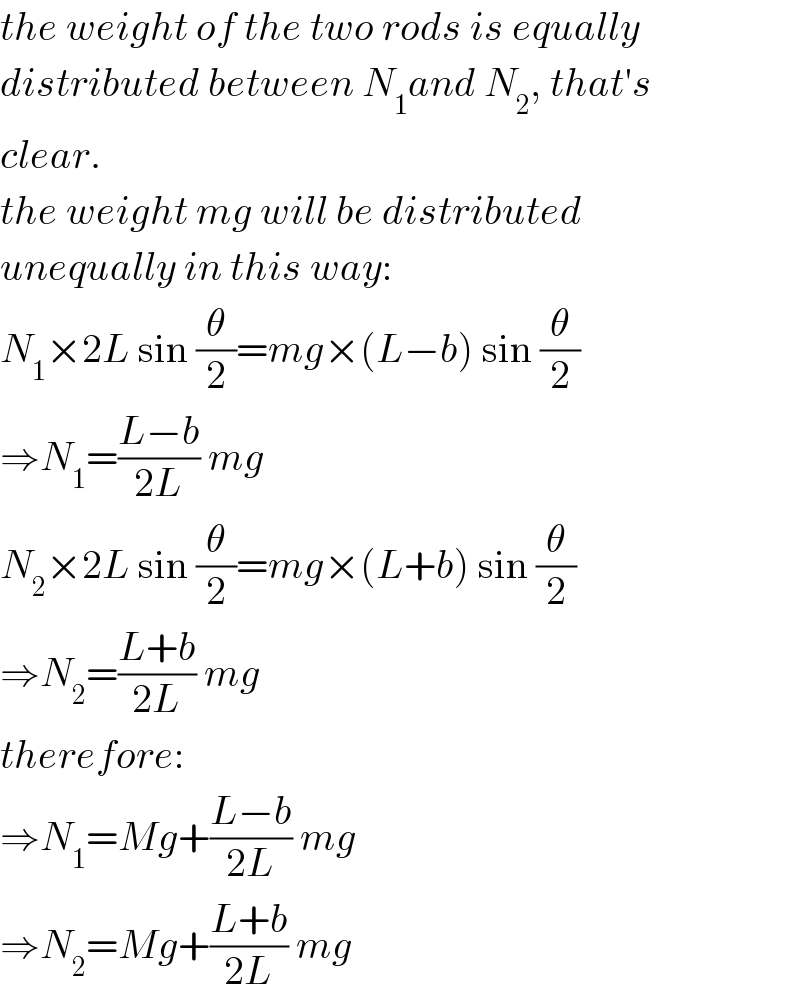
$${the}\:{weight}\:{of}\:{the}\:{two}\:{rods}\:{is}\:{equally} \\ $$$${distributed}\:{between}\:{N}_{\mathrm{1}} {and}\:{N}_{\mathrm{2}} ,\:{that}'{s} \\ $$$${clear}. \\ $$$${the}\:{weight}\:{mg}\:{will}\:{be}\:{distributed}\: \\ $$$${unequally}\:{in}\:{this}\:{way}: \\ $$$${N}_{\mathrm{1}} ×\mathrm{2}{L}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}={mg}×\left({L}−{b}\right)\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow{N}_{\mathrm{1}} =\frac{{L}−{b}}{\mathrm{2}{L}}\:{mg} \\ $$$${N}_{\mathrm{2}} ×\mathrm{2}{L}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}={mg}×\left({L}+{b}\right)\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow{N}_{\mathrm{2}} =\frac{{L}+{b}}{\mathrm{2}{L}}\:{mg} \\ $$$${therefore}: \\ $$$$\Rightarrow{N}_{\mathrm{1}} ={Mg}+\frac{{L}−{b}}{\mathrm{2}{L}}\:{mg} \\ $$$$\Rightarrow{N}_{\mathrm{2}} ={Mg}+\frac{{L}+{b}}{\mathrm{2}{L}}\:{mg} \\ $$
Commented by mr W last updated on 02/Oct/19

$${sir},\:{can}\:{you}\:{check}\:{the}\:{question}\:{again}: \\ $$$${i}\:{think}\:{the}\:{system}\:{can}\:{not}\:{be} \\ $$$${in}\:{equilibrium}. \\ $$$${to}\:{keep}\:{the}\:{equilibrium}\:{it}\:{must}\:{be} \\ $$$$\theta=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mu^{\mathrm{2}} +\mathrm{8}}−\mathrm{1}}{\mathrm{4}} \\ $$$${but}\:{on}\:{the}\:{other}\:{side}\:{it}\:{must}\:{be} \\ $$$$\alpha=\mathrm{90}°−\theta=\frac{\theta}{\mathrm{2}}\:\Rightarrow\theta=\mathrm{60}° \\ $$
Commented by mr W last updated on 03/Oct/19

Commented by ajfour last updated on 04/Oct/19
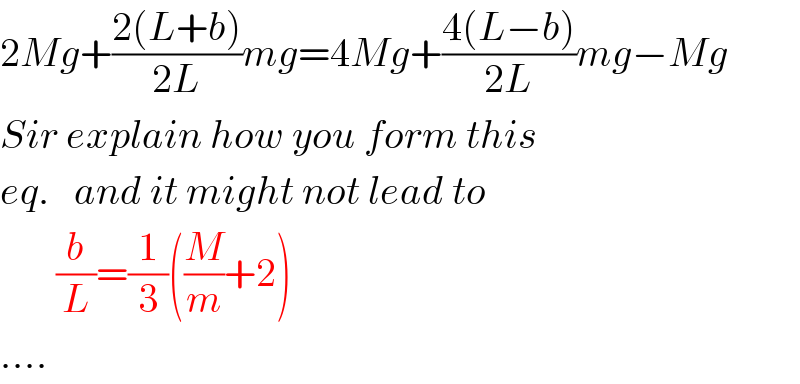
$$\mathrm{2}{Mg}+\frac{\mathrm{2}\left({L}+{b}\right)}{\mathrm{2}{L}}{mg}=\mathrm{4}{Mg}+\frac{\mathrm{4}\left({L}−{b}\right)}{\mathrm{2}{L}}{mg}−{Mg} \\ $$$${Sir}\:{explain}\:{how}\:{you}\:{form}\:{this} \\ $$$${eq}.\:\:\:{and}\:{it}\:{might}\:{not}\:{lead}\:{to} \\ $$$$\:\:\:\:\:\:\:\frac{{b}}{{L}}=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{M}}{{m}}+\mathrm{2}\right) \\ $$$$…. \\ $$
Commented by mr W last updated on 04/Oct/19
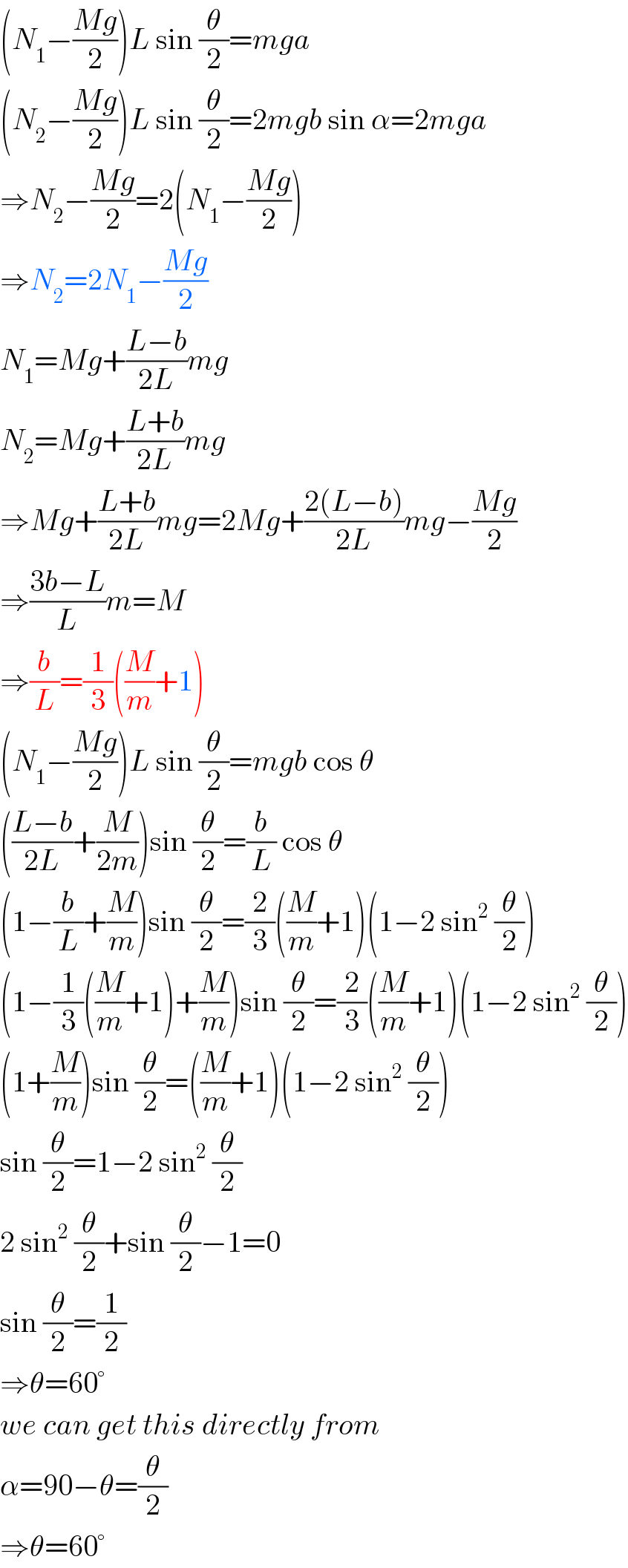
$$\left({N}_{\mathrm{1}} −\frac{{Mg}}{\mathrm{2}}\right){L}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}={mga} \\ $$$$\left({N}_{\mathrm{2}} −\frac{{Mg}}{\mathrm{2}}\right){L}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\mathrm{2}{mgb}\:\mathrm{sin}\:\alpha=\mathrm{2}{mga} \\ $$$$\Rightarrow{N}_{\mathrm{2}} −\frac{{Mg}}{\mathrm{2}}=\mathrm{2}\left({N}_{\mathrm{1}} −\frac{{Mg}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{N}_{\mathrm{2}} =\mathrm{2}{N}_{\mathrm{1}} −\frac{{Mg}}{\mathrm{2}} \\ $$$${N}_{\mathrm{1}} ={Mg}+\frac{{L}−{b}}{\mathrm{2}{L}}{mg} \\ $$$${N}_{\mathrm{2}} ={Mg}+\frac{{L}+{b}}{\mathrm{2}{L}}{mg} \\ $$$$\Rightarrow{Mg}+\frac{{L}+{b}}{\mathrm{2}{L}}{mg}=\mathrm{2}{Mg}+\frac{\mathrm{2}\left({L}−{b}\right)}{\mathrm{2}{L}}{mg}−\frac{{Mg}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{3}{b}−{L}}{{L}}{m}={M} \\ $$$$\Rightarrow\frac{{b}}{{L}}=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{M}}{{m}}+\mathrm{1}\right) \\ $$$$\left({N}_{\mathrm{1}} −\frac{{Mg}}{\mathrm{2}}\right){L}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}={mgb}\:\mathrm{cos}\:\theta \\ $$$$\left(\frac{{L}−{b}}{\mathrm{2}{L}}+\frac{{M}}{\mathrm{2}{m}}\right)\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{{b}}{{L}}\:\mathrm{cos}\:\theta \\ $$$$\left(\mathrm{1}−\frac{{b}}{{L}}+\frac{{M}}{{m}}\right)\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{{M}}{{m}}+\mathrm{1}\right)\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}\right) \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{M}}{{m}}+\mathrm{1}\right)+\frac{{M}}{{m}}\right)\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{{M}}{{m}}+\mathrm{1}\right)\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}\right) \\ $$$$\left(\mathrm{1}+\frac{{M}}{{m}}\right)\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\left(\frac{{M}}{{m}}+\mathrm{1}\right)\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}\right) \\ $$$$\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\mathrm{60}° \\ $$$${we}\:{can}\:{get}\:{this}\:{directly}\:{from} \\ $$$$\alpha=\mathrm{90}−\theta=\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\mathrm{60}° \\ $$
Commented by mr W last updated on 04/Oct/19

$${sorry},\:{i}\:{had}\:{a}\:{typo}\:{in} \\ $$$$\Rightarrow\frac{{b}}{{L}}=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{M}}{{m}}+\mathrm{2}\right) \\ $$$${which}\:{led}\:{to}\:{wrong}\:{conclusion}. \\ $$
Commented by ajfour last updated on 04/Oct/19
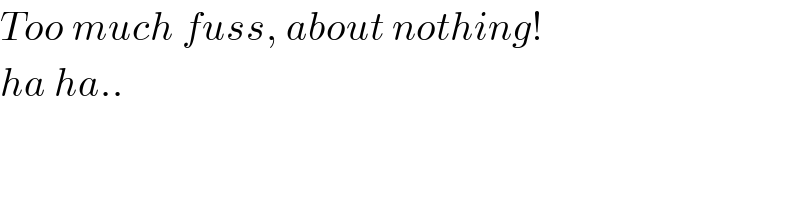
$${Too}\:{much}\:{fuss},\:{about}\:{nothing}! \\ $$$${ha}\:{ha}.. \\ $$
