Menu Close

Question-70163

Tinku Tara 0 Comments
Pin




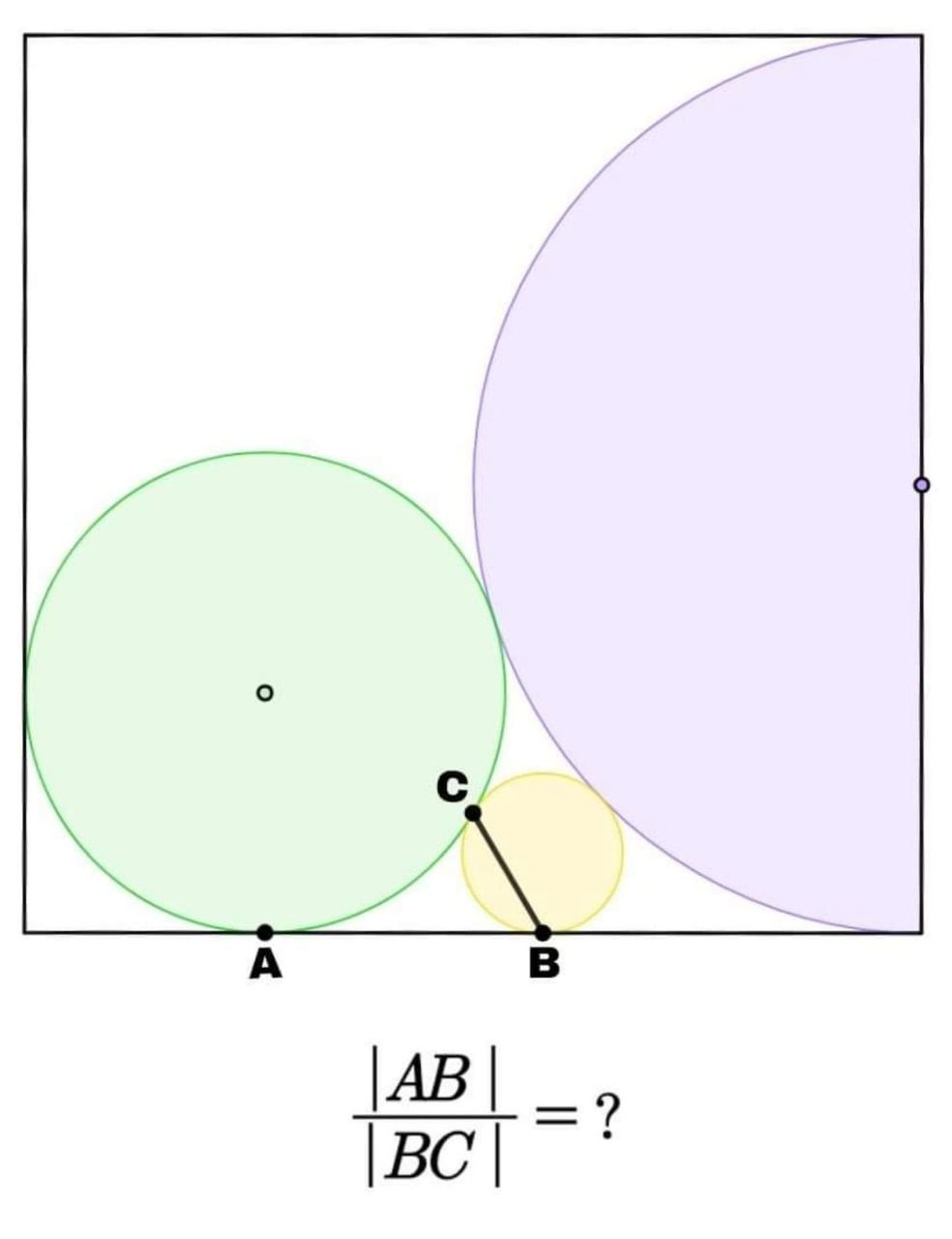
Question Number 70163 by A8;15: last updated on 01/Oct/19
Answered by ajfour last updated on 01/Oct/19
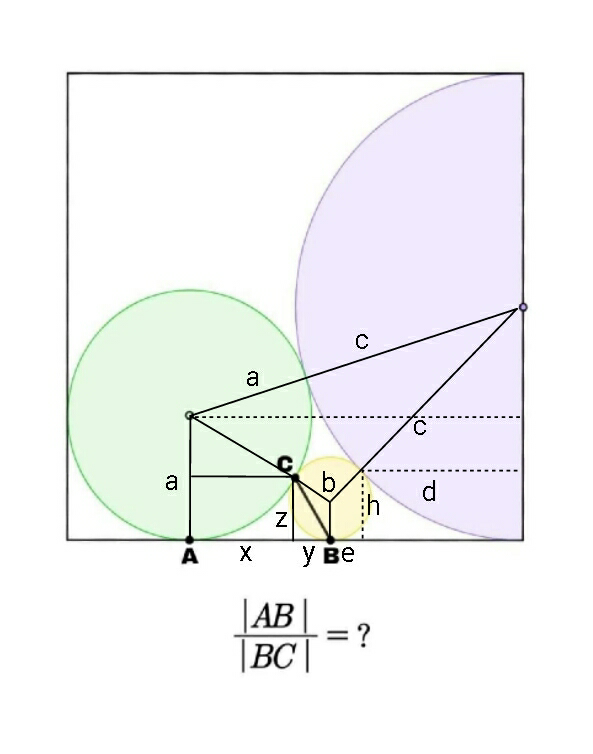
Commented by ajfour last updated on 02/Oct/19
((AB)/(BC))=Q= ((x+y)/( (√(y^2 +z^2 )))) x+y+e+d=2c−a ....(i) (x/y)=(a/b) & (e/d)=(b/c) ...(ii) (2c−a)^2 =4ac ⇒ 4((c/a))^2 −8((c/a))+1=0 ⇒ (c/a)=λ=((8+(√(64−16)))/8) =1+((√3)/2) (e+d)^2 =4bc d((b/c)+1)=2(√(bc)) ⇒ d=((2c(√(bc)))/(b+c)) , e=((2b(√(bc)))/(b+c)) ((a−z)/(z−b))=(a/b) ⇒ ab−bz=az−ab ⇒ z=((2ab)/(a+b)) y^2 = b^2 −(z−b)^2 = 2bz−z^2 = ((4ab^2 (a+b)−4a^2 b^2 )/((a+b)^2 )) y=((2b(√(ab)))/(a+b)) ; x= ((2a(√(ab)))/(a+b)) Q=((AB)/(BC))=((x+y)/( (√(y^2 +z^2 )))) = ((2(√(ab)))/( (√((((2b(√(ab)))/(a+b)))^2 +(((2ab)/(a+b)))^2 )))) =((2(a+b)(√(ab)))/( (√(4ab^2 (b+a))))) = (√(1+(a/b))) Now taking up (i) x+y+e+d=2c−a 2(√(ab))+2(√(bc))=2c−a ⇒ 2(√(b/a))+2(√(λ((b/a)))) =2λ−1 ⇒ 2(√(b/a))(1+(√λ))=2λ−1 (√(b/a)) = ((2λ−1)/(2(1+(√λ)))) Q= ((AB)/(BC)) = (√(1+((4(1+(√λ))^2 )/((2λ−1)^2 )))) λ=1+((√3)/2) .
$$\:\:\frac{{AB}}{{BC}}={Q}=\:\frac{{x}+{y}}{\:\sqrt{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }}\: \\ $$$${x}+{y}+{e}+{d}=\mathrm{2}{c}−{a}\:\:\:\:\:\:….\left({i}\right) \\ $$$$\frac{{x}}{{y}}=\frac{{a}}{{b}}\:\:\:\&\:\:\:\frac{\boldsymbol{{e}}}{{d}}=\frac{{b}}{{c}}\:\:\:\:\:\:\:…\left({ii}\right) \\ $$$$\:\:\left(\mathrm{2}{c}−{a}\right)^{\mathrm{2}} =\mathrm{4}{ac} \\ $$$$\Rightarrow\:\:\:\mathrm{4}\left(\frac{{c}}{{a}}\right)^{\mathrm{2}} −\mathrm{8}\left(\frac{{c}}{{a}}\right)+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\frac{{c}}{{a}}=\lambda=\frac{\mathrm{8}+\sqrt{\mathrm{64}−\mathrm{16}}}{\mathrm{8}}\:=\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\:\:\:\left(\boldsymbol{{e}}+{d}\right)^{\mathrm{2}} =\mathrm{4}{bc} \\ $$$$\:\:\:\:{d}\left(\frac{{b}}{{c}}+\mathrm{1}\right)=\mathrm{2}\sqrt{{bc}} \\ $$$$\Rightarrow\:\:{d}=\frac{\mathrm{2}{c}\sqrt{{bc}}}{{b}+{c}}\:\:\:\:,\:\:\boldsymbol{{e}}=\frac{\mathrm{2}{b}\sqrt{{bc}}}{{b}+{c}} \\ $$$$\:\frac{{a}−{z}}{{z}−{b}}=\frac{{a}}{{b}}\:\:\:\Rightarrow\:\:{ab}−{bz}={az}−{ab} \\ $$$$\Rightarrow\:\:\:\:{z}=\frac{\mathrm{2}{ab}}{{a}+{b}} \\ $$$$\:\:\:{y}^{\mathrm{2}} =\:{b}^{\mathrm{2}} −\left({z}−{b}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{2}{bz}−{z}^{\mathrm{2}} \:=\:\frac{\mathrm{4}{ab}^{\mathrm{2}} \left({a}+{b}\right)−\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} } \\ $$$$\:\:{y}=\frac{\mathrm{2}{b}\sqrt{{ab}}}{{a}+{b}}\:\:\:\:;\:\:\:{x}=\:\frac{\mathrm{2}{a}\sqrt{{ab}}}{{a}+{b}} \\ $$$$\:\:{Q}=\frac{{AB}}{{BC}}=\frac{{x}+{y}}{\:\sqrt{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }}\: \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{2}\sqrt{{ab}}}{\:\sqrt{\left(\frac{\mathrm{2}{b}\sqrt{{ab}}}{{a}+{b}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}{ab}}{{a}+{b}}\right)^{\mathrm{2}} }} \\ $$$$\:\:\:=\frac{\mathrm{2}\left({a}+{b}\right)\sqrt{{ab}}}{\:\sqrt{\mathrm{4}{ab}^{\mathrm{2}} \left({b}+{a}\right)}}\:=\:\sqrt{\mathrm{1}+\frac{{a}}{{b}}} \\ $$$${Now}\:\:{taking}\:{up}\:\left({i}\right) \\ $$$$\:\:\:\:{x}+{y}+{e}+{d}=\mathrm{2}{c}−{a} \\ $$$$\:\:\:\mathrm{2}\sqrt{{ab}}+\mathrm{2}\sqrt{{bc}}=\mathrm{2}{c}−{a} \\ $$$$\Rightarrow\:\:\mathrm{2}\sqrt{\frac{{b}}{{a}}}+\mathrm{2}\sqrt{\lambda\left(\frac{{b}}{{a}}\right)}\:=\mathrm{2}\lambda−\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{2}\sqrt{\frac{{b}}{{a}}}\left(\mathrm{1}+\sqrt{\lambda}\right)=\mathrm{2}\lambda−\mathrm{1} \\ $$$$\:\:\:\sqrt{\frac{{b}}{{a}}}\:=\:\frac{\mathrm{2}\lambda−\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\sqrt{\lambda}\right)} \\ $$$${Q}=\:\frac{{AB}}{{BC}}\:=\:\sqrt{\mathrm{1}+\frac{\mathrm{4}\left(\mathrm{1}+\sqrt{\lambda}\right)^{\mathrm{2}} }{\left(\mathrm{2}\lambda−\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$\:\:\:\:\lambda=\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *