Question Number 70253 by oyemi kemewari last updated on 02/Oct/19
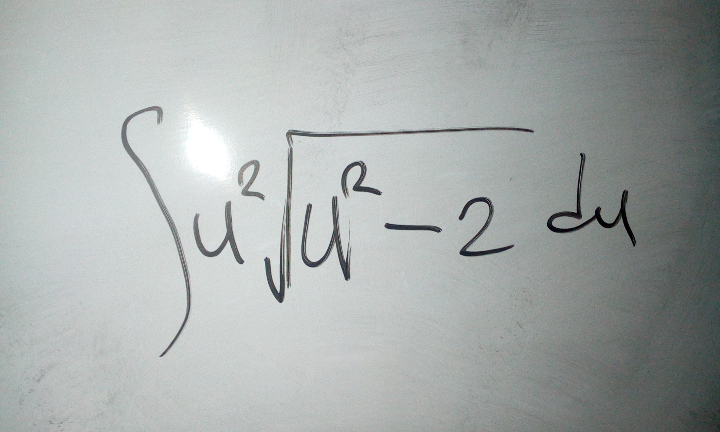
Commented by mathmax by abdo last updated on 02/Oct/19
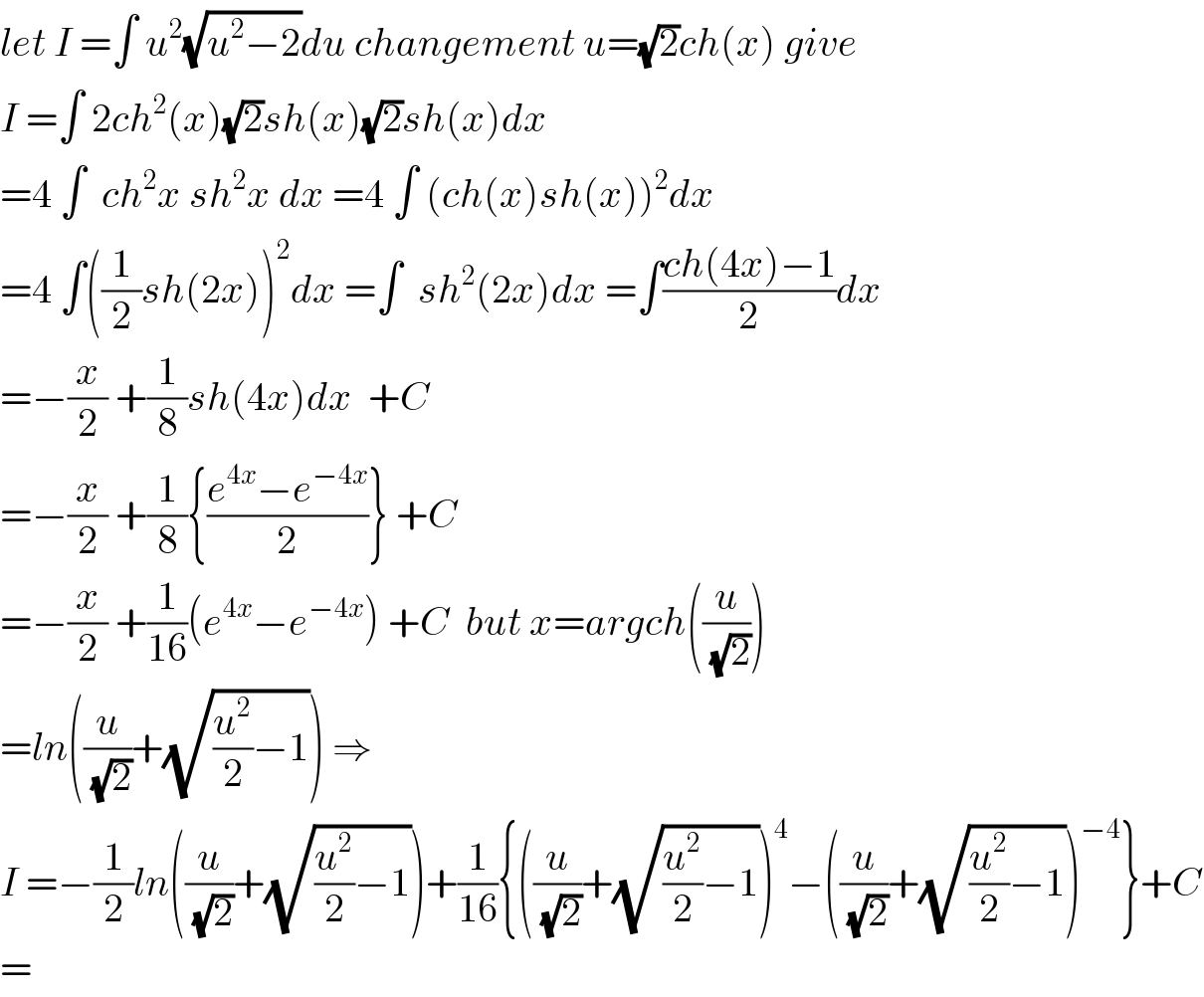
$${let}\:{I}\:=\int\:{u}^{\mathrm{2}} \sqrt{{u}^{\mathrm{2}} −\mathrm{2}}{du}\:{changement}\:{u}=\sqrt{\mathrm{2}}{ch}\left({x}\right)\:{give} \\ $$$${I}\:=\int\:\mathrm{2}{ch}^{\mathrm{2}} \left({x}\right)\sqrt{\mathrm{2}}{sh}\left({x}\right)\sqrt{\mathrm{2}}{sh}\left({x}\right){dx} \\ $$$$=\mathrm{4}\:\int\:\:{ch}^{\mathrm{2}} {x}\:{sh}^{\mathrm{2}} {x}\:{dx}\:=\mathrm{4}\:\int\:\left({ch}\left({x}\right){sh}\left({x}\right)\right)^{\mathrm{2}} {dx} \\ $$$$=\mathrm{4}\:\int\left(\frac{\mathrm{1}}{\mathrm{2}}{sh}\left(\mathrm{2}{x}\right)\right)^{\mathrm{2}} {dx}\:=\int\:\:{sh}^{\mathrm{2}} \left(\mathrm{2}{x}\right){dx}\:=\int\frac{{ch}\left(\mathrm{4}{x}\right)−\mathrm{1}}{\mathrm{2}}{dx} \\ $$$$=−\frac{{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{8}}{sh}\left(\mathrm{4}{x}\right){dx}\:\:+{C} \\ $$$$=−\frac{{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{8}}\left\{\frac{{e}^{\mathrm{4}{x}} −{e}^{−\mathrm{4}{x}} }{\mathrm{2}}\right\}\:+{C} \\ $$$$=−\frac{{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{16}}\left({e}^{\mathrm{4}{x}} −{e}^{−\mathrm{4}{x}} \right)\:+{C}\:\:{but}\:{x}={argch}\left(\frac{{u}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$={ln}\left(\frac{{u}}{\:\sqrt{\mathrm{2}}}+\sqrt{\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}\right)\:\Rightarrow \\ $$$${I}\:=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{u}}{\:\sqrt{\mathrm{2}}}+\sqrt{\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}\right)+\frac{\mathrm{1}}{\mathrm{16}}\left\{\left(\frac{{u}}{\:\sqrt{\mathrm{2}}}+\sqrt{\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}\right)^{\mathrm{4}} −\left(\frac{{u}}{\:\sqrt{\mathrm{2}}}+\sqrt{\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}\right)^{−\mathrm{4}} \right\}+{C} \\ $$$$= \\ $$
Commented by oyemi kemewari last updated on 02/Oct/19
thanks you slr
Commented by mathmax by abdo last updated on 03/Oct/19
$${you}\:{are}\:{welcome}. \\ $$
