Question-7026

Question Number 7026 by Tawakalitu. last updated on 07/Aug/16

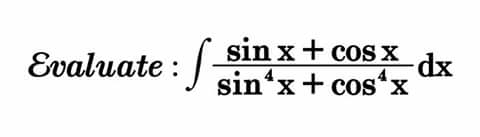
Commented by Yozzii last updated on 07/Aug/16

Write ∫((sinx+cosx)/(sin^4 x+cos^4 x))dx=∫((sinx)/(sin^4 x+cos^4 x))dx+∫((cosx)/(sin^4 x+cos^4 x))dx. Evaluate each integral by the following steps (1) Substitute u=cosx in ∫((sinx)/(sin^4 x+cos^4 x))dx where sin^4 x+cos^4 x=2cos^4 x−2cos^2 x+1, {and substitute k=sinx in ∫((cosx)/(sin^4 x+cos^4 x))dx where sin^4 x+cos^4 x=2sin^4 x−2sin^2 x+1.} (2) Complete the square in the denominators of the resulting integrand. e.g 2u^4 −2u^2 +1=0.5((2u^2 −1)^2 +1). (3)Apply the identity z^2 +1=(z−i)(z+i) with z=2u^2 −1 for the first integrand for example. ⇒(2u^2 −1)^2 +1=(2u^2 −1−i)(2u^2 −1+i) or (2u^2 −1)^2 +1=((√2)u−(√(1+i)))((√2)u+(√(1+i)))(2u^2 −1+i) (4)Split (2/((2u^2 −1)^2 +1)) into partial fractions. Solve for a,b,c,d∈C in (2/((2u^2 −1)^2 +1))≡(a/( (√2)u−(√(1+i))))+(b/( (√2)u+(√(1+i))))+((cu+d)/(2u^2 +i−1)) (5)Then integrate and simplify as usual e.g: ∫((sinx)/(sin^4 x+cos^4 x))dx=−∫{(a/( (√2)u−(√(1+i))))+(b/( (√2)u+(√(1+i))))+((cu+d)/(2u^2 +i−1))}du=−F(u)+C=−F(cosx)+C where (d/du)F(u)=(a/( (√2)u−(√(1+i))))+(b/( (√2)u+(√(1+i))))+((cu+d)/(2u^2 +i−1)). −−−−−−−−−−−−−−−−−−−−−−−−−− For ∫((cosx)/(sin^4 x+cos^4 x))dx, this turns out to be ∫((cosx)/(sin^4 x+cos^4 x))dx=F(k)+T=F(sinx)+T ∴ ∫((sinx+cosx)/(sin^4 x+cos^4 x))dx=F(sinx)−F(cosx)+constant.

$${Write}\:\int\frac{{sinx}+{cosx}}{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}}{dx}=\int\frac{{sinx}}{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}}{dx}+\int\frac{{cosx}}{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}}{dx}. \\ $$$${Evaluate}\:{each}\:{integral}\:{by}\:{the}\:{following}\:{steps} \\ $$$$\left(\mathrm{1}\right)\:{Substitute}\:{u}={cosx}\:{in}\:\int\frac{{sinx}}{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}}{dx} \\ $$$${where}\:{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}=\mathrm{2}{cos}^{\mathrm{4}} {x}−\mathrm{2}{cos}^{\mathrm{2}} {x}+\mathrm{1},\: \\ $$$$\left\{{and}\:{substitute}\:{k}={sinx}\:{in}\:\int\frac{{cosx}}{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}}{dx}\right. \\ $$$$\left.{where}\:{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}=\mathrm{2}{sin}^{\mathrm{4}} {x}−\mathrm{2}{sin}^{\mathrm{2}} {x}+\mathrm{1}.\right\} \\ $$$$\left(\mathrm{2}\right)\:{Complete}\:{the}\:{square}\:{in}\:{the}\:{denominators}\:{of} \\ $$$${the}\:{resulting}\:{integrand}. \\ $$$${e}.{g}\:\mathrm{2}{u}^{\mathrm{4}} −\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}.\mathrm{5}\left(\left(\mathrm{2}{u}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right). \\ $$$$\left(\mathrm{3}\right){Apply}\:{the}\:{identity}\:{z}^{\mathrm{2}} +\mathrm{1}=\left({z}−{i}\right)\left({z}+{i}\right) \\ $$$${with}\:{z}=\mathrm{2}{u}^{\mathrm{2}} −\mathrm{1}\:{for}\:{the}\:{first}\:{integrand}\: \\ $$$${for}\:{example}. \\ $$$$\Rightarrow\left(\mathrm{2}{u}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}=\left(\mathrm{2}{u}^{\mathrm{2}} −\mathrm{1}−{i}\right)\left(\mathrm{2}{u}^{\mathrm{2}} −\mathrm{1}+{i}\right) \\ $$$${or}\:\left(\mathrm{2}{u}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}=\left(\sqrt{\mathrm{2}}{u}−\sqrt{\mathrm{1}+{i}}\right)\left(\sqrt{\mathrm{2}}{u}+\sqrt{\mathrm{1}+{i}}\right)\left(\mathrm{2}{u}^{\mathrm{2}} −\mathrm{1}+{i}\right) \\ $$$$\left(\mathrm{4}\right){Split}\:\frac{\mathrm{2}}{\left(\mathrm{2}{u}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\:{into}\:{partial}\:{fractions}. \\ $$$${Solve}\:{for}\:{a},{b},{c},{d}\in\mathbb{C}\:{in} \\ $$$$\frac{\mathrm{2}}{\left(\mathrm{2}{u}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\equiv\frac{{a}}{\:\sqrt{\mathrm{2}}{u}−\sqrt{\mathrm{1}+{i}}}+\frac{{b}}{\:\sqrt{\mathrm{2}}{u}+\sqrt{\mathrm{1}+{i}}}+\frac{{cu}+{d}}{\mathrm{2}{u}^{\mathrm{2}} +{i}−\mathrm{1}} \\ $$$$\left(\mathrm{5}\right){Then}\:{integrate}\:{and}\:{simplify}\:{as}\:{usual} \\ $$$${e}.{g}:\:\int\frac{{sinx}}{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}}{dx}=−\int\left\{\frac{{a}}{\:\sqrt{\mathrm{2}}{u}−\sqrt{\mathrm{1}+{i}}}+\frac{{b}}{\:\sqrt{\mathrm{2}}{u}+\sqrt{\mathrm{1}+{i}}}+\frac{{cu}+{d}}{\mathrm{2}{u}^{\mathrm{2}} +{i}−\mathrm{1}}\right\}{du}=−{F}\left({u}\right)+{C}=−{F}\left({cosx}\right)+{C} \\ $$$${where}\:\frac{{d}}{{du}}{F}\left({u}\right)=\frac{{a}}{\:\sqrt{\mathrm{2}}{u}−\sqrt{\mathrm{1}+{i}}}+\frac{{b}}{\:\sqrt{\mathrm{2}}{u}+\sqrt{\mathrm{1}+{i}}}+\frac{{cu}+{d}}{\mathrm{2}{u}^{\mathrm{2}} +{i}−\mathrm{1}}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${For}\:\int\frac{{cosx}}{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}}{dx},\:{this}\:{turns}\:{out}\:{to}\:{be} \\ $$$$\int\frac{{cosx}}{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}}{dx}={F}\left({k}\right)+{T}={F}\left({sinx}\right)+{T} \\ $$$$\therefore\:\int\frac{{sinx}+{cosx}}{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}}{dx}={F}\left({sinx}\right)−{F}\left({cosx}\right)+{constant}. \\ $$

Commented by Tawakalitu. last updated on 07/Aug/16