Question Number 70277 by mr W last updated on 02/Oct/19

Answered by mind is power last updated on 02/Oct/19
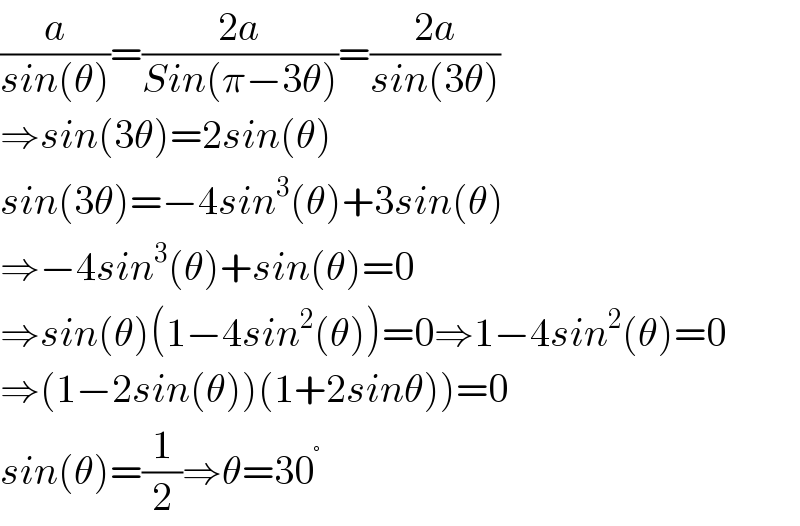
$$\frac{{a}}{{sin}\left(\theta\right)}=\frac{\mathrm{2}{a}}{{Sin}\left(\pi−\mathrm{3}\theta\right)}=\frac{\mathrm{2}{a}}{{sin}\left(\mathrm{3}\theta\right)} \\ $$$$\Rightarrow{sin}\left(\mathrm{3}\theta\right)=\mathrm{2}{sin}\left(\theta\right) \\ $$$${sin}\left(\mathrm{3}\theta\right)=−\mathrm{4}{sin}^{\mathrm{3}} \left(\theta\right)+\mathrm{3}{sin}\left(\theta\right) \\ $$$$\Rightarrow−\mathrm{4}{sin}^{\mathrm{3}} \left(\theta\right)+{sin}\left(\theta\right)=\mathrm{0} \\ $$$$\Rightarrow{sin}\left(\theta\right)\left(\mathrm{1}−\mathrm{4}{sin}^{\mathrm{2}} \left(\theta\right)\right)=\mathrm{0}\Rightarrow\mathrm{1}−\mathrm{4}{sin}^{\mathrm{2}} \left(\theta\right)=\mathrm{0} \\ $$$$\left.\Rightarrow\left(\mathrm{1}−\mathrm{2}{sin}\left(\theta\right)\right)\left(\mathrm{1}+\mathrm{2}{sin}\theta\right)\right)=\mathrm{0} \\ $$$${sin}\left(\theta\right)=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\theta=\mathrm{30}^{°} \\ $$
Commented by mr W last updated on 02/Oct/19
��
Commented by mr W last updated on 02/Oct/19
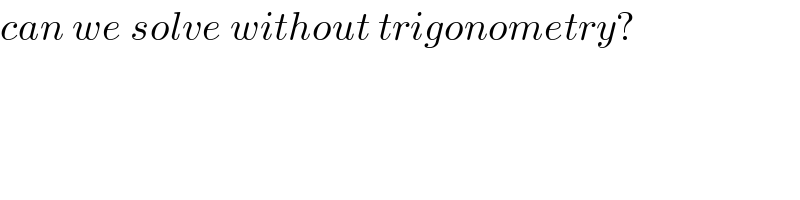
$${can}\:{we}\:{solve}\:{without}\:{trigonometry}? \\ $$
Commented by mind is power last updated on 03/Oct/19

$${i}\:{will}\:{Try}\:{sir} \\ $$
Answered by som(math1967) last updated on 03/Oct/19

$${Construct}\:{bisector}\:{of}\:\angle{B}\left(\mathrm{2}\alpha\right)\:{AD} \\ $$$$\therefore\frac{{AD}}{{DC}}=\frac{{a}}{\mathrm{2}{a}}=\frac{\mathrm{1}}{\mathrm{2}}\:\therefore{AD}=\frac{\mathrm{1}}{\mathrm{3}}{AC} \\ $$$${again}\:\bigtriangleup{ABC}\sim\bigtriangleup{ABD} \\ $$$$\therefore\frac{{AB}}{{AD}}=\frac{{AC}}{{AB}} \\ $$$$\therefore{AB}^{\mathrm{2}} ={AD}×{AC}=\frac{\mathrm{1}}{\mathrm{3}}{AC}^{\mathrm{2}} \\ $$$${AC}^{\mathrm{2}} =\mathrm{3}{AB}^{\mathrm{2}} =\mathrm{3}{a}^{\mathrm{2}} \\ $$$${AB}^{\mathrm{2}} +{AC}^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} =\mathrm{4}{a}^{\mathrm{2}} ={BC}^{\mathrm{2}} \\ $$$$\therefore\angle{A}=\mathrm{90}°\:\therefore\alpha+\mathrm{2}\alpha=\mathrm{90} \\ $$$$\:\alpha=\mathrm{30}\: \\ $$
Commented by som(math1967) last updated on 03/Oct/19

Commented by som(math1967) last updated on 03/Oct/19
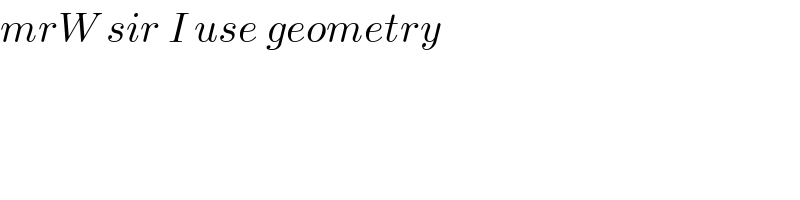
$${mrW}\:{sir}\:{I}\:{use}\:{geometry}\: \\ $$
Commented by mr W last updated on 03/Oct/19
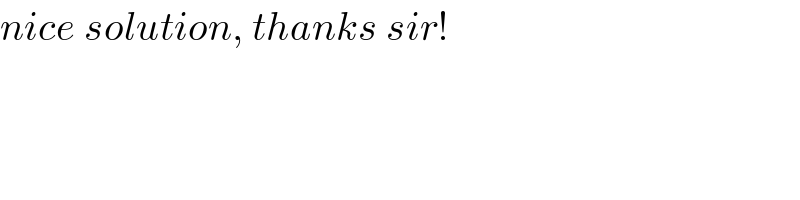
$${nice}\:{solution},\:{thanks}\:{sir}! \\ $$
