Question Number 70298 by naka3546 last updated on 03/Oct/19
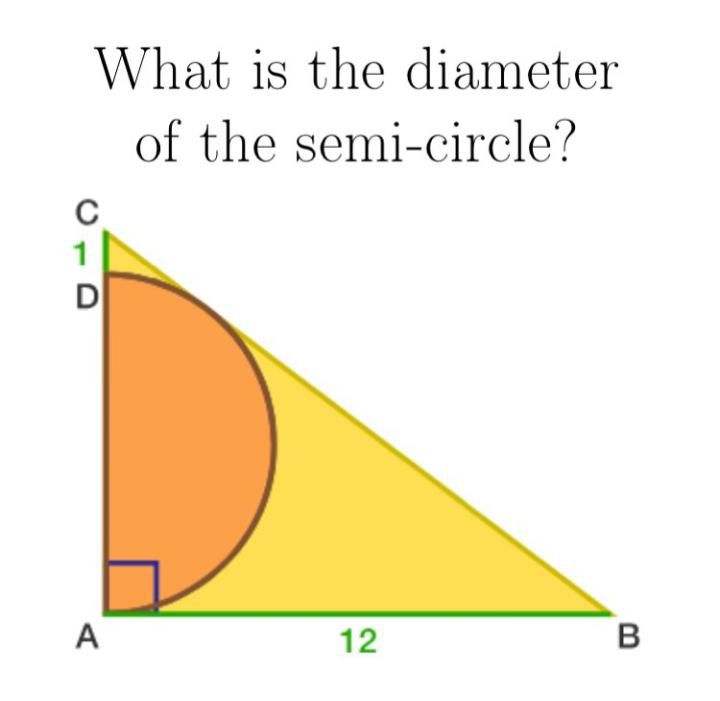
Answered by mr W last updated on 03/Oct/19
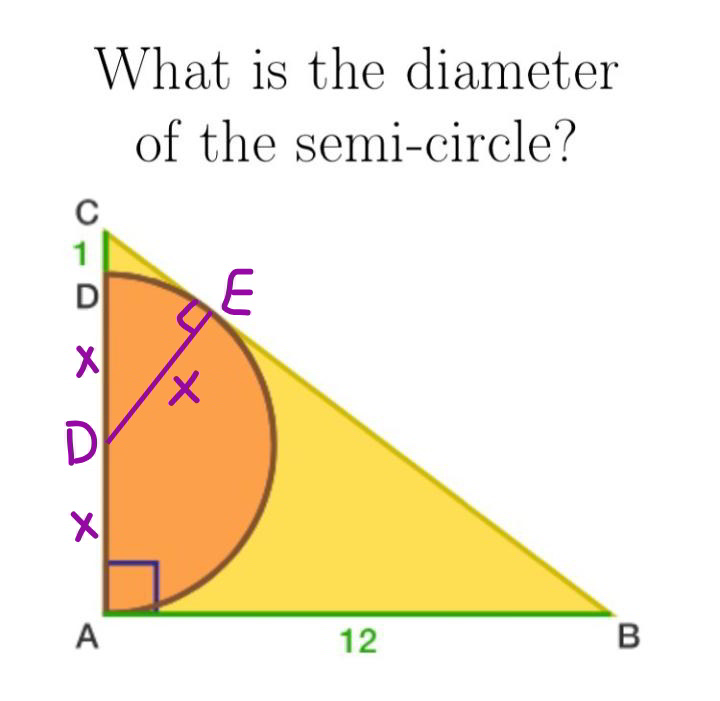
Commented by mr W last updated on 03/Oct/19

$${CE}=\sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} }=\sqrt{\mathrm{2}{x}+\mathrm{1}} \\ $$$$\frac{{CE}}{{ED}}=\frac{{CA}}{{AB}} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{2}{x}+\mathrm{1}}}{{x}}=\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{12}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{x}}=\frac{\sqrt{\mathrm{2}{x}+\mathrm{1}}}{\mathrm{12}} \\ $$$$\Rightarrow{x}\sqrt{\mathrm{2}{x}+\mathrm{1}}=\mathrm{12} \\ $$$$\Rightarrow{x}^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{1}\right)=\mathrm{144} \\ $$$$\Rightarrow\mathrm{2}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{144}=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\mathrm{4}\right)\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{36}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{4} \\ $$$$\Rightarrow{diameter}=\mathrm{8} \\ $$
