Question-7031

Question Number 7031 by Tawakalitu. last updated on 07/Aug/16

Commented by FilupSmith last updated on 07/Aug/16

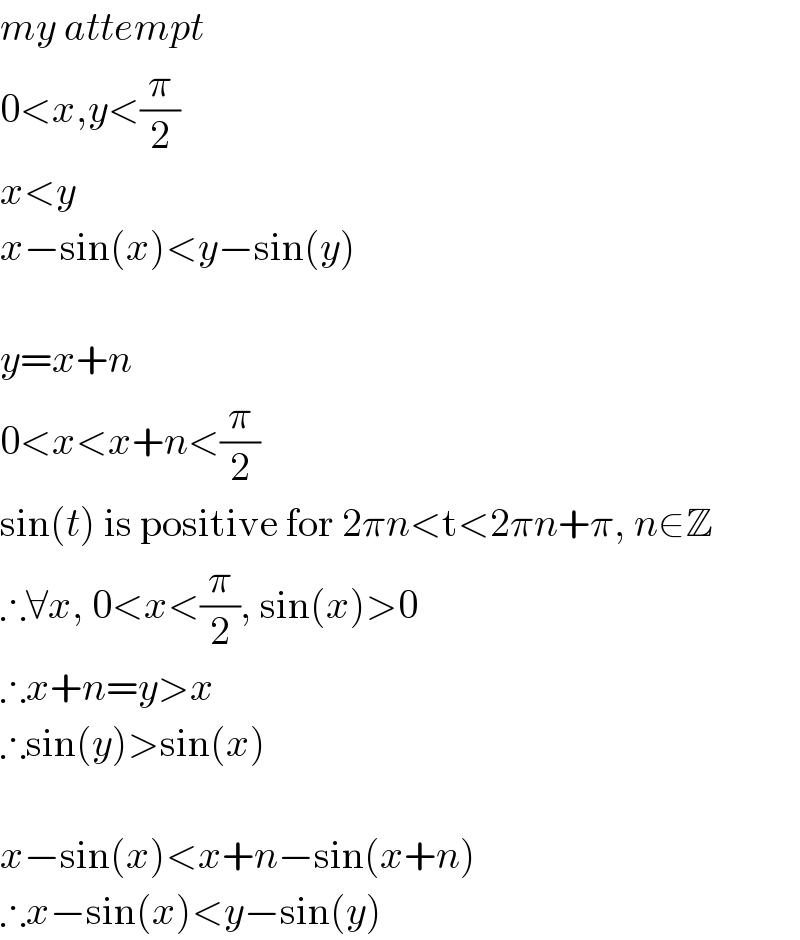
my attempt 0<x,y<(π/2) x<y x−sin(x)<y−sin(y) y=x+n 0<x<x+n<(π/2) sin(t) is positive for 2πn<t<2πn+π, n∈Z ∴∀x, 0<x<(π/2), sin(x)>0 ∴x+n=y>x ∴sin(y)>sin(x) x−sin(x)<x+n−sin(x+n) ∴x−sin(x)<y−sin(y)

$${my}\:{attempt} \\ $$$$\mathrm{0}<{x},{y}<\frac{\pi}{\mathrm{2}} \\ $$$${x}<{y} \\ $$$${x}−\mathrm{sin}\left({x}\right)<{y}−\mathrm{sin}\left({y}\right) \\ $$$$\: \\ $$$${y}={x}+{n} \\ $$$$\mathrm{0}<{x}<{x}+{n}<\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{sin}\left({t}\right)\:\mathrm{is}\:\mathrm{positive}\:\mathrm{for}\:\mathrm{2}\pi{n}<\mathrm{t}<\mathrm{2}\pi{n}+\pi,\:{n}\in\mathbb{Z} \\ $$$$\therefore\forall{x},\:\mathrm{0}<{x}<\frac{\pi}{\mathrm{2}},\:\mathrm{sin}\left({x}\right)>\mathrm{0} \\ $$$$\therefore{x}+{n}={y}>{x} \\ $$$$\therefore\mathrm{sin}\left({y}\right)>\mathrm{sin}\left({x}\right) \\ $$$$ \\ $$$${x}−\mathrm{sin}\left({x}\right)<{x}+{n}−\mathrm{sin}\left({x}+{n}\right) \\ $$$$\therefore{x}−\mathrm{sin}\left({x}\right)<{y}−\mathrm{sin}\left({y}\right) \\ $$

Commented by Tawakalitu. last updated on 07/Aug/16

$${I}\:{appreciate}.\:{Thank}\:{you}. \\ $$

Commented by prakash jain last updated on 07/Aug/16

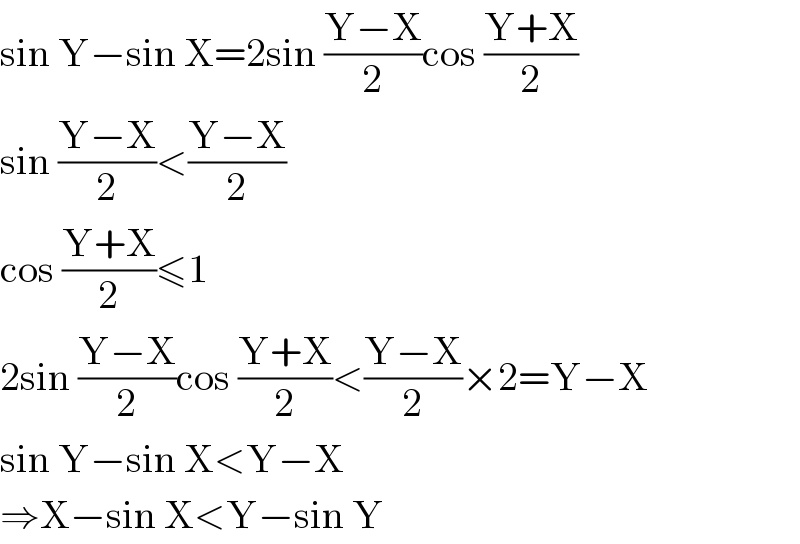
sin Y−sin X=2sin ((Y−X)/2)cos ((Y+X)/2) sin ((Y−X)/2)<((Y−X)/2) cos ((Y+X)/2)≤1 2sin ((Y−X)/2)cos ((Y+X)/2)<((Y−X)/2)×2=Y−X sin Y−sin X<Y−X ⇒X−sin X<Y−sin Y

$$\mathrm{sin}\:\mathrm{Y}−\mathrm{sin}\:\mathrm{X}=\mathrm{2sin}\:\frac{\mathrm{Y}−\mathrm{X}}{\mathrm{2}}\mathrm{cos}\:\frac{\mathrm{Y}+\mathrm{X}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\frac{\mathrm{Y}−\mathrm{X}}{\mathrm{2}}<\frac{\mathrm{Y}−\mathrm{X}}{\mathrm{2}}\: \\ $$$$\mathrm{cos}\:\frac{\mathrm{Y}+\mathrm{X}}{\mathrm{2}}\leqslant\mathrm{1} \\ $$$$\mathrm{2sin}\:\frac{\mathrm{Y}−\mathrm{X}}{\mathrm{2}}\mathrm{cos}\:\frac{\mathrm{Y}+\mathrm{X}}{\mathrm{2}}<\frac{\mathrm{Y}−\mathrm{X}}{\mathrm{2}}×\mathrm{2}=\mathrm{Y}−\mathrm{X} \\ $$$$\mathrm{sin}\:\mathrm{Y}−\mathrm{sin}\:\mathrm{X}<\mathrm{Y}−\mathrm{X} \\ $$$$\Rightarrow\mathrm{X}−\mathrm{sin}\:\mathrm{X}<\mathrm{Y}−\mathrm{sin}\:\mathrm{Y} \\ $$

Commented by prakash jain last updated on 07/Aug/16

To prove the relation geometrically you can use the same contruction as used to prove sin C −sin D formula.

$$\mathrm{To}\:\mathrm{prove}\:\mathrm{the}\:\mathrm{relation}\:\mathrm{geometrically}\:\mathrm{you} \\ $$$$\mathrm{can}\:\mathrm{use}\:\mathrm{the}\:\mathrm{same}\:\mathrm{contruction}\:\mathrm{as}\:\mathrm{used}\:\mathrm{to} \\ $$$$\mathrm{prove}\:\mathrm{sin}\:\mathrm{C}\:−\mathrm{sin}\:\mathrm{D}\:\mathrm{formula}. \\ $$

Commented by Tawakalitu. last updated on 08/Aug/16

$${Thanks}\:{so}\:{much}\:{for}\:{your}\:{help} \\ $$

Answered by Yozzii last updated on 08/Aug/16

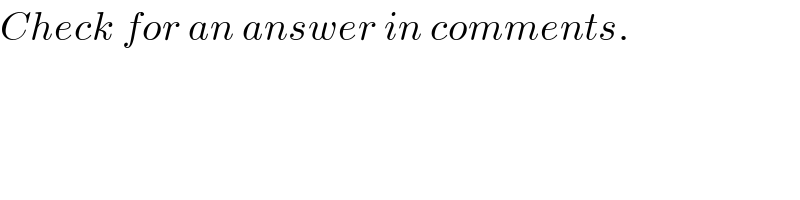
$${Check}\:{for}\:{an}\:{answer}\:{in}\:{comments}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply