Question Number 70429 by TawaTawa last updated on 04/Oct/19

Commented by TawaTawa last updated on 04/Oct/19
If ABCD is a square, AH is the tangent of the sector BEF at G,
AG:GH = 7, and DH = 2. Find the area of the square
Commented by MJS last updated on 04/Oct/19

$${AG}:{GH}=\mathrm{7}??? \\ $$$$\mathrm{is}\:\mathrm{it}\:\mathrm{1}:\mathrm{7}\:\mathrm{or}\:\mathrm{7}:\mathrm{1}? \\ $$
Commented by TawaTawa last updated on 04/Oct/19

$$\mathrm{7}:\mathrm{1}\:\:\mathrm{sir} \\ $$
Commented by MJS last updated on 04/Oct/19

$$\mathrm{ok}\:\mathrm{but}\:\mathrm{then}\:\mathrm{the}\:\mathrm{picture}\:\mathrm{is}\:\mathrm{wrong}…\:\mathrm{it}\:\mathrm{looks} \\ $$$$\mathrm{like}\:\mathrm{1}:\mathrm{7} \\ $$
Commented by TawaTawa last updated on 04/Oct/19

$$\mathrm{Help}\:\mathrm{me}\:\mathrm{do}\:\mathrm{it}\:\mathrm{like}\:\:\:\mathrm{1}:\mathrm{7}\:\:\mathrm{sir} \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$
Commented by MJS last updated on 04/Oct/19
$$\mathrm{will}\:\mathrm{try}\:\mathrm{with}\:\mathrm{7}:\mathrm{1}\:\mathrm{later} \\ $$
Answered by MJS last updated on 04/Oct/19

$$\mathrm{triangles}\:{HDA}\:\mathrm{and}\:{AGB}\:\mathrm{are}\:\mathrm{similar} \\ $$$${AG}^{\mathrm{2}} +{GB}^{\mathrm{2}} ={BA}^{\mathrm{2}} \\ $$$${HD}^{\mathrm{2}} +{DA}^{\mathrm{2}} ={AH}^{\mathrm{2}} \\ $$$${AG}={x};\:{GH}=\mathrm{7}{x};\:{HD}=\mathrm{2};\:{BA}={DA}={s};\:{GB}={r} \\ $$$$ \\ $$$${x}^{\mathrm{2}} +{r}^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\mathrm{4}+{s}^{\mathrm{2}} =\mathrm{64}{x}^{\mathrm{2}} \\ $$$$\Rightarrow\:{r}^{\mathrm{2}} =\frac{\mathrm{63}}{\mathrm{64}}{s}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$ \\ $$$$\frac{{AG}}{{HD}}=\frac{{GB}}{{DA}}=\frac{{BA}}{{AH}} \\ $$$$\frac{{x}}{\mathrm{2}}=\frac{{r}}{{s}}=\frac{{s}}{\mathrm{8}{x}} \\ $$$$\Rightarrow\:{r}=\frac{\sqrt{{s}^{\mathrm{3}} }}{\mathrm{4}} \\ $$$$ \\ $$$$\Rightarrow\:\frac{{s}^{\mathrm{3}} }{\mathrm{16}}=\frac{\mathrm{63}}{\mathrm{64}}{s}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{16}} \\ $$$${s}^{\mathrm{3}} −\frac{\mathrm{63}}{\mathrm{4}}{s}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:{s}=−\frac{\mathrm{1}}{\mathrm{4}}\vee{s}=\mathrm{8}\pm\mathrm{2}\sqrt{\mathrm{15}} \\ $$$$\mathrm{but}\:{s}\geqslant\mathrm{2}\:\Rightarrow\:{s}=\mathrm{8}+\mathrm{2}\sqrt{\mathrm{15}} \\ $$$${r}=\frac{\mathrm{7}\sqrt{\mathrm{5}}}{\mathrm{2}}+\frac{\mathrm{9}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${x}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${area}={s}^{\mathrm{2}} =\mathrm{124}+\mathrm{32}\sqrt{\mathrm{15}} \\ $$
Commented by TawaTawa last updated on 04/Oct/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by MJS last updated on 04/Oct/19

$$\mathrm{if}\:\mathrm{we}\:\mathrm{start}\:\mathrm{with}\:\mathrm{7}:\mathrm{1}\:\mathrm{we}\:\mathrm{get}\:{s}=−\frac{\mathrm{7}}{\mathrm{4}}\:\mathrm{and}\:{r}\notin\mathbb{R} \\ $$
Commented by TawaTawa last updated on 04/Oct/19
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$
Commented by ajfour last updated on 04/Oct/19
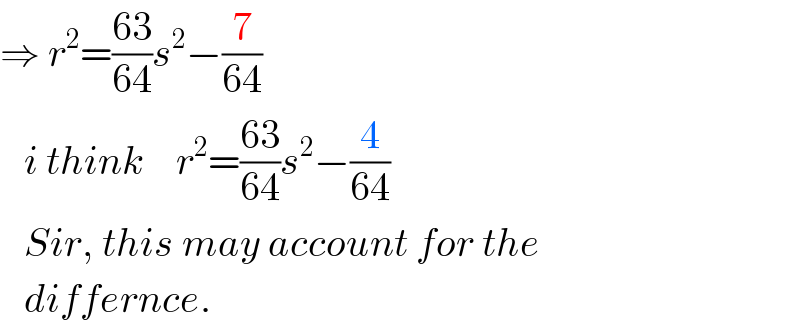
$$\Rightarrow\:{r}^{\mathrm{2}} =\frac{\mathrm{63}}{\mathrm{64}}{s}^{\mathrm{2}} −\frac{\mathrm{7}}{\mathrm{64}} \\ $$$$\:\:\:{i}\:{think}\:\:\:\:{r}^{\mathrm{2}} =\frac{\mathrm{63}}{\mathrm{64}}{s}^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{64}} \\ $$$$\:\:\:{Sir},\:{this}\:{may}\:{account}\:{for}\:{the} \\ $$$$\:\:\:{differnce}. \\ $$
Commented by MJS last updated on 04/Oct/19

$$\mathrm{you}'\mathrm{re}\:\mathrm{right},\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{typo}…\:\mathrm{thank}\:\mathrm{you} \\ $$
Answered by ajfour last updated on 04/Oct/19
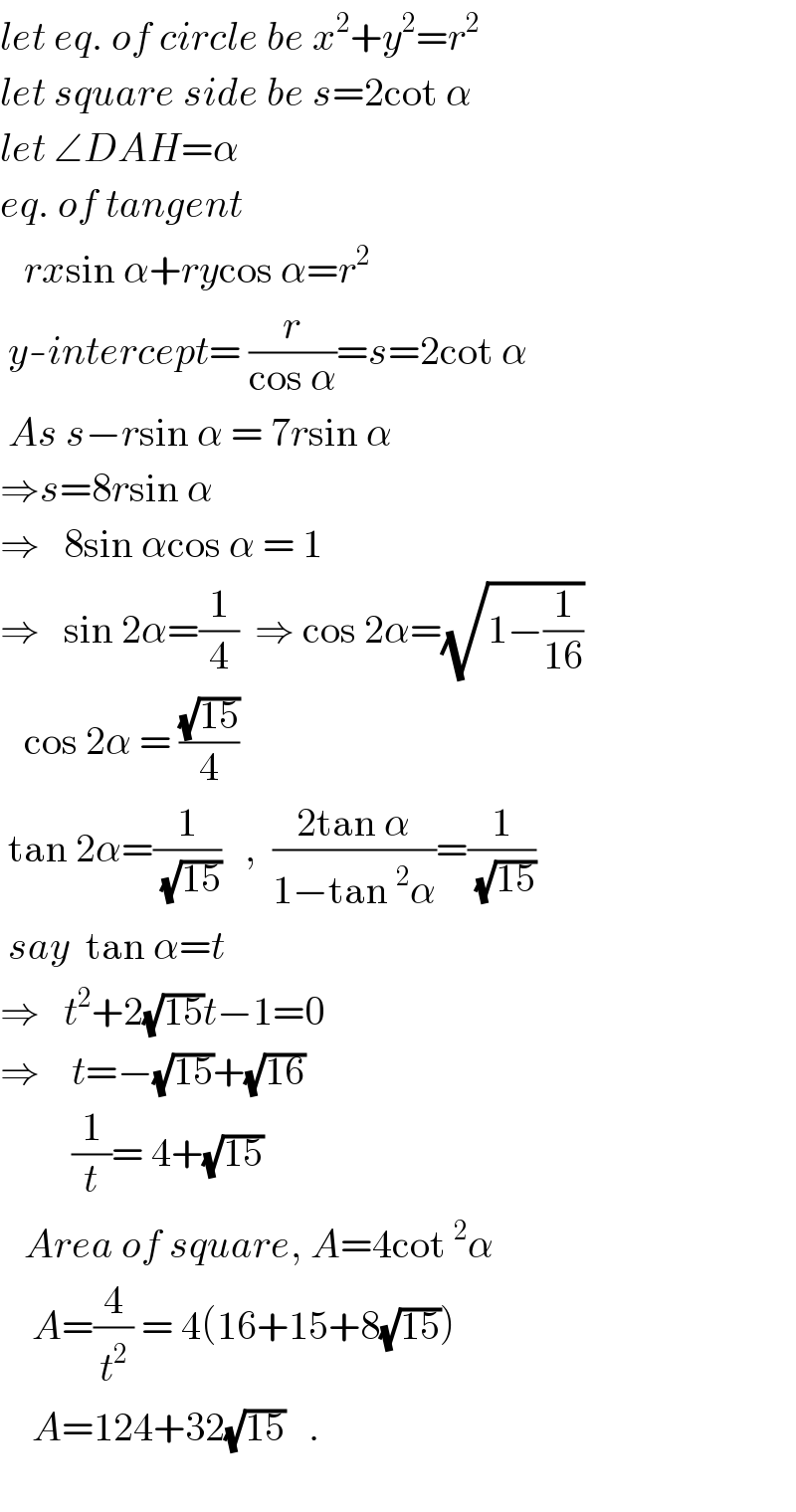
$${let}\:{eq}.\:{of}\:{circle}\:{be}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${let}\:{square}\:{side}\:{be}\:{s}=\mathrm{2cot}\:\alpha \\ $$$${let}\:\angle{DAH}=\alpha \\ $$$${eq}.\:{of}\:{tangent}\:\: \\ $$$$\:\:\:{rx}\mathrm{sin}\:\alpha+{ry}\mathrm{cos}\:\alpha={r}^{\mathrm{2}} \\ $$$$\:{y}-{intercept}=\:\frac{{r}}{\mathrm{cos}\:\alpha}={s}=\mathrm{2cot}\:\alpha \\ $$$$\:{As}\:{s}−{r}\mathrm{sin}\:\alpha\:=\:\mathrm{7}{r}\mathrm{sin}\:\alpha \\ $$$$\Rightarrow{s}=\mathrm{8}{r}\mathrm{sin}\:\alpha \\ $$$$\Rightarrow\:\:\:\mathrm{8sin}\:\alpha\mathrm{cos}\:\alpha\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\:\:\mathrm{sin}\:\mathrm{2}\alpha=\frac{\mathrm{1}}{\mathrm{4}}\:\:\Rightarrow\:\mathrm{cos}\:\mathrm{2}\alpha=\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{16}}} \\ $$$$\:\:\:\mathrm{cos}\:\mathrm{2}\alpha\:=\:\frac{\sqrt{\mathrm{15}}}{\mathrm{4}} \\ $$$$\:\mathrm{tan}\:\mathrm{2}\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{15}}}\:\:\:,\:\:\frac{\mathrm{2tan}\:\alpha}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \alpha}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{15}}} \\ $$$$\:{say}\:\:\mathrm{tan}\:\alpha={t} \\ $$$$\Rightarrow\:\:\:{t}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{15}}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:{t}=−\sqrt{\mathrm{15}}+\sqrt{\mathrm{16}} \\ $$$$\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{t}}=\:\mathrm{4}+\sqrt{\mathrm{15}} \\ $$$$\:\:\:{Area}\:{of}\:{square},\:{A}=\mathrm{4cot}\:^{\mathrm{2}} \alpha \\ $$$$\:\:\:\:{A}=\frac{\mathrm{4}}{{t}^{\mathrm{2}} }\:=\:\mathrm{4}\left(\mathrm{16}+\mathrm{15}+\mathrm{8}\sqrt{\mathrm{15}}\right) \\ $$$$\:\:\:\:{A}=\mathrm{124}+\mathrm{32}\sqrt{\mathrm{15}}\:\:\:. \\ $$$$\:\: \\ $$
Commented by TawaTawa last updated on 04/Oct/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by MJS last updated on 04/Oct/19
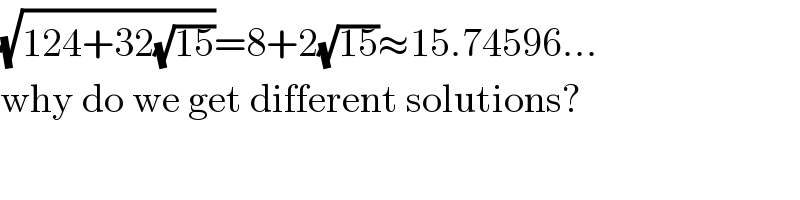
$$\sqrt{\mathrm{124}+\mathrm{32}\sqrt{\mathrm{15}}}=\mathrm{8}+\mathrm{2}\sqrt{\mathrm{15}}\approx\mathrm{15}.\mathrm{74596}… \\ $$$$\mathrm{why}\:\mathrm{do}\:\mathrm{we}\:\mathrm{get}\:\mathrm{different}\:\mathrm{solutions}? \\ $$
Answered by Henri Boucatchou last updated on 05/Oct/19

$$\boldsymbol{{What}}'\boldsymbol{{s}}\:\:\boldsymbol{{happening}}\:\:\boldsymbol{{here}},\:\:\boldsymbol{{people}}\:\:\boldsymbol{{text}}\:\:\boldsymbol{{pictures}}\:\:\boldsymbol{{without}}\:\:\boldsymbol{{any}}\:\:\boldsymbol{{question}}?? \\ $$
