Question Number 70590 by behi83417@gmail.com last updated on 05/Oct/19
Commented by behi83417@gmail.com last updated on 05/Oct/19

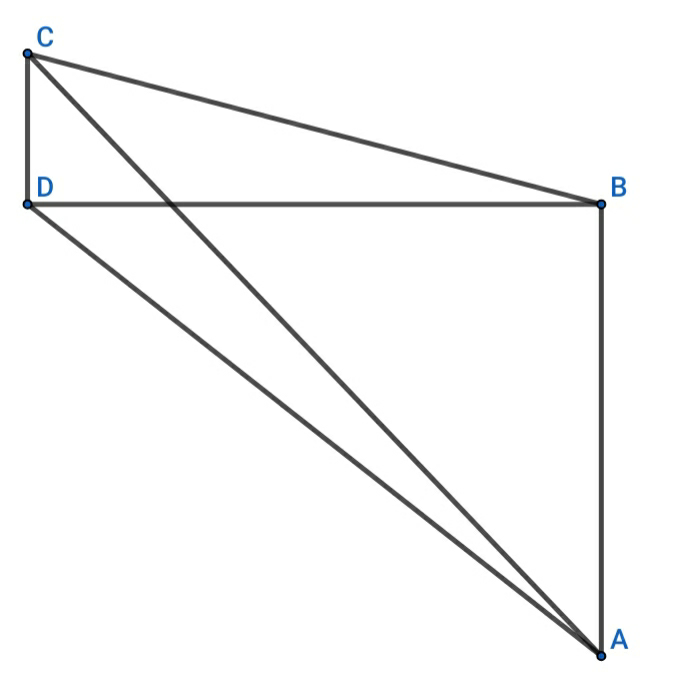
$$\mathrm{convex}\:\mathrm{ABCD},\mathrm{is}\:\mathrm{given}\:\mathrm{with}: \\ $$$$\boldsymbol{\mathrm{S}}_{\mathrm{ABCD}} =\boldsymbol{\mathrm{p}}\:\:\:,\:\:\:\:\:\mathrm{AB}+\mathrm{BD}+\mathrm{DC}=\boldsymbol{\mathrm{q}}\:\:\:. \\ $$$$\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{maximum}}\:\boldsymbol{\mathrm{value}}\:\boldsymbol{\mathrm{for}}:\:\boldsymbol{\mathrm{AC}},\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{terms}} \\ $$$$\boldsymbol{\mathrm{of}}:\:\:\boldsymbol{\mathrm{p}}\:\:\boldsymbol{\mathrm{and}}\:\:\boldsymbol{\mathrm{q}}. \\ $$
Answered by mr W last updated on 06/Oct/19
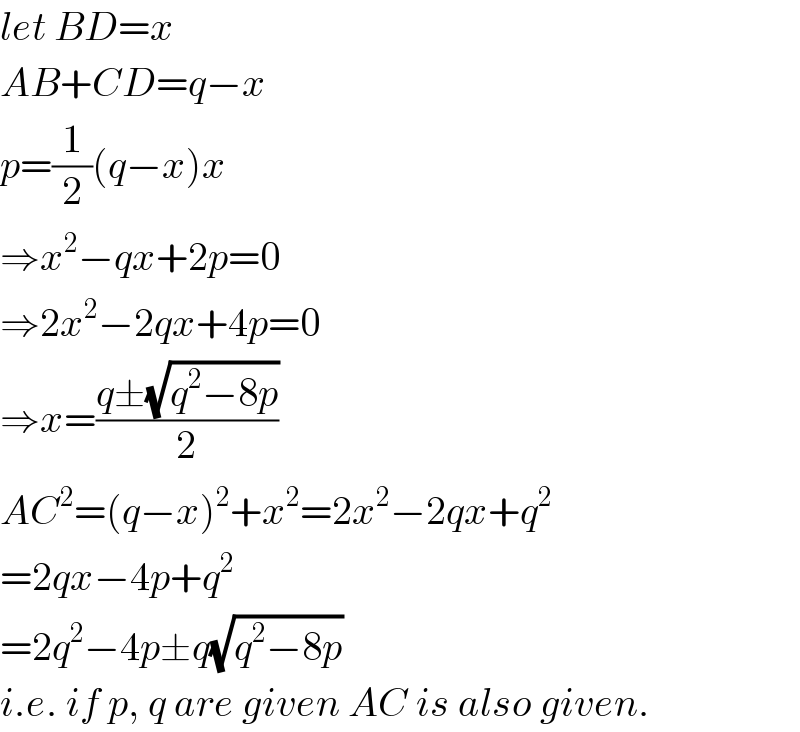
$${let}\:{BD}={x} \\ $$$${AB}+{CD}={q}−{x} \\ $$$${p}=\frac{\mathrm{1}}{\mathrm{2}}\left({q}−{x}\right){x} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −{qx}+\mathrm{2}{p}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{qx}+\mathrm{4}{p}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{{q}\pm\sqrt{{q}^{\mathrm{2}} −\mathrm{8}{p}}}{\mathrm{2}} \\ $$$${AC}^{\mathrm{2}} =\left({q}−{x}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} =\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{qx}+{q}^{\mathrm{2}} \\ $$$$=\mathrm{2}{qx}−\mathrm{4}{p}+{q}^{\mathrm{2}} \\ $$$$=\mathrm{2}{q}^{\mathrm{2}} −\mathrm{4}{p}\pm{q}\sqrt{{q}^{\mathrm{2}} −\mathrm{8}{p}} \\ $$$${i}.{e}.\:{if}\:{p},\:{q}\:{are}\:{given}\:{AC}\:{is}\:{also}\:{given}. \\ $$
Commented by behi83417@gmail.com last updated on 06/Oct/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{master}.\mathrm{i}\:\mathrm{think}\:\mathrm{for} \\ $$$$\mathrm{maximum}\:\mathrm{value}\:\mathrm{for}\:\mathrm{AC},\mathrm{it}\:\mathrm{should}\:\mathrm{be}: \\ $$$$\measuredangle\mathrm{ABD}=\measuredangle\mathrm{BDC}=\mathrm{90}^{\bullet} \\ $$
