Question Number 70694 by oyemi kemewari last updated on 07/Oct/19
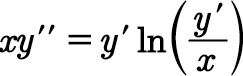
Answered by mind is power last updated on 07/Oct/19
![let ((y′)/x)=u ⇒y′=xu⇒y′′=u+xu′ xy′′=xu+x^2 u′ xu+x^2 u′=xuln(u) ⇒u+xu′=uln(u) ⇒((u′)/(ulnu −u))=(1/x) ⇒((u′)/(u(ln(u)−1)))=(1/x) ⇒≥ { ((ln(ln(u)−1)=ln(∣x∣)+c u(0)>e^1 )),((ln(1−ln(u))=ln(∣x∣)+v if u(0)∈]0,e^1 ⌊)) :} ⇒u=e^(k∣x∣+1) =((y′)/x)⇒y′=xe^(k∣x∣+1) if x>0 y=∫xe^(−kx+1) =[((−x)/k)e^(−kx+1) ]+(1/k)∫e^(−kx+1) dx=−(1/k^2 )(kx+1)e^(−kx+1)](https://www.tinkutara.com/question/Q70703.png)
$${let}\:\frac{{y}'}{{x}}={u} \\ $$$$\Rightarrow{y}'={xu}\Rightarrow{y}''={u}+{xu}' \\ $$$${xy}''={xu}+{x}^{\mathrm{2}} {u}' \\ $$$${xu}+{x}^{\mathrm{2}} {u}'={xuln}\left({u}\right) \\ $$$$\Rightarrow{u}+{xu}'={uln}\left({u}\right) \\ $$$$\Rightarrow\frac{{u}'}{{ulnu}\:−{u}}=\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow\frac{{u}'}{{u}\left({ln}\left({u}\right)−\mathrm{1}\right)}=\frac{\mathrm{1}}{{x}}\:\:\:\:\:\: \\ $$$$\Rightarrow\geqslant\begin{cases}{{ln}\left({ln}\left({u}\right)−\mathrm{1}\right)={ln}\left(\mid{x}\mid\right)+{c}\:\:\:{u}\left(\mathrm{0}\right)>{e}^{\mathrm{1}} }\\{\left.{ln}\left(\mathrm{1}−{ln}\left({u}\right)\right)={ln}\left(\mid{x}\mid\right)+{v}\:{if}\:{u}\left(\mathrm{0}\right)\in\right]\mathrm{0},{e}^{\mathrm{1}} \lfloor}\end{cases} \\ $$$$\Rightarrow{u}={e}^{{k}\mid{x}\mid+\mathrm{1}} =\frac{{y}'}{{x}}\Rightarrow{y}'={xe}^{{k}\mid{x}\mid+\mathrm{1}} \\ $$$${if}\:{x}>\mathrm{0} \\ $$$${y}=\int{xe}^{−{kx}+\mathrm{1}} =\left[\frac{−{x}}{{k}}{e}^{−{kx}+\mathrm{1}} \right]+\frac{\mathrm{1}}{{k}}\int{e}^{−{kx}+\mathrm{1}} {dx}=−\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\left({kx}+\mathrm{1}\right){e}^{−{kx}+\mathrm{1}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by oyemi kemewari last updated on 07/Oct/19
thank you sir
