Menu Close

Question-70757

Tinku Tara 0 Comments
Pin




Question Number 70757 by MJS last updated on 08/Oct/19
.
$$. \\ $$
Commented by TawaTawa last updated on 07/Oct/19
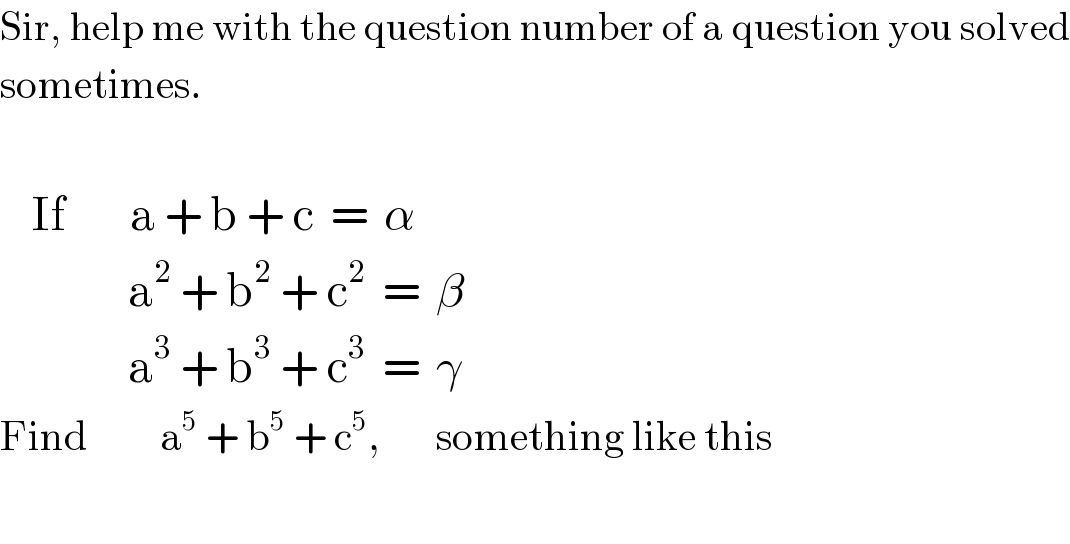
Sir, help me with the question number of a question you solved sometimes. If a + b + c = α a^2 + b^2 + c^2 = β a^3 + b^3 + c^3 = γ Find a^5 + b^5 + c^5 , something like this
$$\mathrm{Sir},\:\mathrm{help}\:\mathrm{me}\:\mathrm{with}\:\mathrm{the}\:\mathrm{question}\:\mathrm{number}\:\mathrm{of}\:\mathrm{a}\:\mathrm{question}\:\mathrm{you}\:\mathrm{solved} \\ $$$$\mathrm{sometimes}. \\ $$$$ \\ $$$$\:\:\:\:\mathrm{If}\:\:\:\:\:\:\:\:\mathrm{a}\:+\:\mathrm{b}\:+\:\mathrm{c}\:\:=\:\:\alpha \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}^{\mathrm{2}} \:+\:\mathrm{b}^{\mathrm{2}} \:+\:\mathrm{c}^{\mathrm{2}} \:\:=\:\:\beta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}^{\mathrm{3}} \:+\:\mathrm{b}^{\mathrm{3}} \:+\:\mathrm{c}^{\mathrm{3}} \:\:=\:\:\gamma \\ $$$$\mathrm{Find}\:\:\:\:\:\:\:\:\:\mathrm{a}^{\mathrm{5}} \:+\:\mathrm{b}^{\mathrm{5}} \:+\:\mathrm{c}^{\mathrm{5}} ,\:\:\:\:\:\:\:\mathrm{something}\:\mathrm{like}\:\mathrm{this} \\ $$$$ \\ $$
Commented by MJS last updated on 07/Oct/19
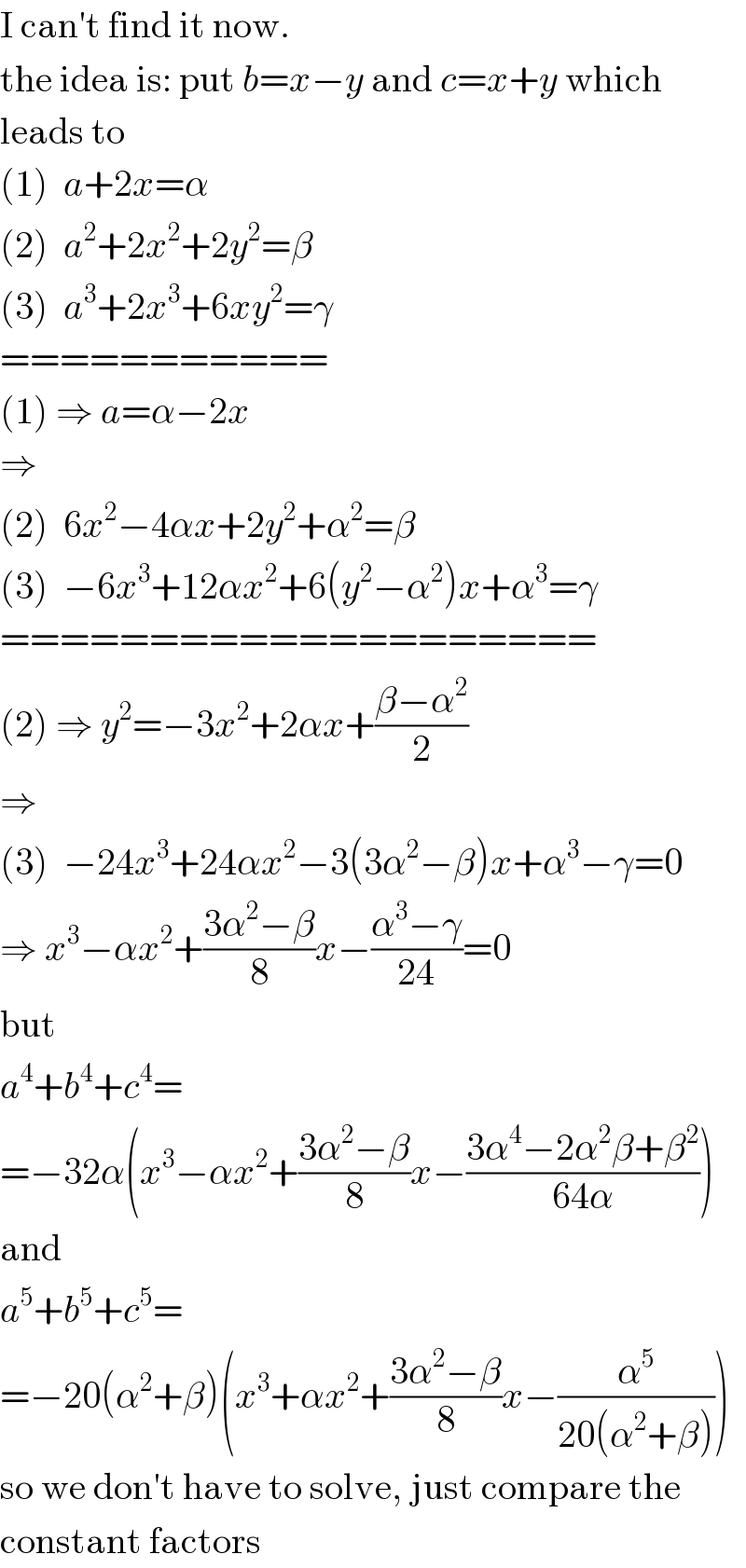
I can′t find it now. the idea is: put b=x−y and c=x+y which leads to (1) a+2x=α (2) a^2 +2x^2 +2y^2 =β (3) a^3 +2x^3 +6xy^2 =γ =========== (1) ⇒ a=α−2x ⇒ (2) 6x^2 −4αx+2y^2 +α^2 =β (3) −6x^3 +12αx^2 +6(y^2 −α^2 )x+α^3 =γ ==================== (2) ⇒ y^2 =−3x^2 +2αx+((β−α^2 )/2) ⇒ (3) −24x^3 +24αx^2 −3(3α^2 −β)x+α^3 −γ=0 ⇒ x^3 −αx^2 +((3α^2 −β)/8)x−((α^3 −γ)/(24))=0 but a^4 +b^4 +c^4 = =−32α(x^3 −αx^2 +((3α^2 −β)/8)x−((3α^4 −2α^2 β+β^2 )/(64α))) and a^5 +b^5 +c^5 = =−20(α^2 +β)(x^3 +αx^2 +((3α^2 −β)/8)x−(α^5 /(20(α^2 +β)))) so we don′t have to solve, just compare the constant factors
$$\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{find}\:\mathrm{it}\:\mathrm{now}. \\ $$$$\mathrm{the}\:\mathrm{idea}\:\mathrm{is}:\:\mathrm{put}\:{b}={x}−{y}\:\mathrm{and}\:{c}={x}+{y}\:\mathrm{which} \\ $$$$\mathrm{leads}\:\mathrm{to} \\ $$$$\left(\mathrm{1}\right)\:\:{a}+\mathrm{2}{x}=\alpha \\ $$$$\left(\mathrm{2}\right)\:\:{a}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} =\beta \\ $$$$\left(\mathrm{3}\right)\:\:{a}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{3}} +\mathrm{6}{xy}^{\mathrm{2}} =\gamma \\ $$$$=========== \\ $$$$\left(\mathrm{1}\right)\:\Rightarrow\:{a}=\alpha−\mathrm{2}{x} \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{2}\right)\:\:\mathrm{6}{x}^{\mathrm{2}} −\mathrm{4}\alpha{x}+\mathrm{2}{y}^{\mathrm{2}} +\alpha^{\mathrm{2}} =\beta \\ $$$$\left(\mathrm{3}\right)\:\:−\mathrm{6}{x}^{\mathrm{3}} +\mathrm{12}\alpha{x}^{\mathrm{2}} +\mathrm{6}\left({y}^{\mathrm{2}} −\alpha^{\mathrm{2}} \right){x}+\alpha^{\mathrm{3}} =\gamma \\ $$$$==================== \\ $$$$\left(\mathrm{2}\right)\:\Rightarrow\:{y}^{\mathrm{2}} =−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}\alpha{x}+\frac{\beta−\alpha^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{3}\right)\:\:−\mathrm{24}{x}^{\mathrm{3}} +\mathrm{24}\alpha{x}^{\mathrm{2}} −\mathrm{3}\left(\mathrm{3}\alpha^{\mathrm{2}} −\beta\right){x}+\alpha^{\mathrm{3}} −\gamma=\mathrm{0} \\ $$$$\Rightarrow\:{x}^{\mathrm{3}} −\alpha{x}^{\mathrm{2}} +\frac{\mathrm{3}\alpha^{\mathrm{2}} −\beta}{\mathrm{8}}{x}−\frac{\alpha^{\mathrm{3}} −\gamma}{\mathrm{24}}=\mathrm{0} \\ $$$$\mathrm{but} \\ $$$${a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} = \\ $$$$=−\mathrm{32}\alpha\left({x}^{\mathrm{3}} −\alpha{x}^{\mathrm{2}} +\frac{\mathrm{3}\alpha^{\mathrm{2}} −\beta}{\mathrm{8}}{x}−\frac{\mathrm{3}\alpha^{\mathrm{4}} −\mathrm{2}\alpha^{\mathrm{2}} \beta+\beta^{\mathrm{2}} }{\mathrm{64}\alpha}\right) \\ $$$$\mathrm{and} \\ $$$${a}^{\mathrm{5}} +{b}^{\mathrm{5}} +{c}^{\mathrm{5}} = \\ $$$$=−\mathrm{20}\left(\alpha^{\mathrm{2}} +\beta\right)\left({x}^{\mathrm{3}} +\alpha{x}^{\mathrm{2}} +\frac{\mathrm{3}\alpha^{\mathrm{2}} −\beta}{\mathrm{8}}{x}−\frac{\alpha^{\mathrm{5}} }{\mathrm{20}\left(\alpha^{\mathrm{2}} +\beta\right)}\right) \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve},\:\mathrm{just}\:\mathrm{compare}\:\mathrm{the} \\ $$$$\mathrm{constant}\:\mathrm{factors} \\ $$
Commented by TawaTawa last updated on 07/Oct/19
God bless you sir, i appreciate
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{appreciate} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *