Question-70784

Question Number 70784 by rajesh4661kumar@gmail.com last updated on 08/Oct/19

Commented by MJS last updated on 08/Oct/19

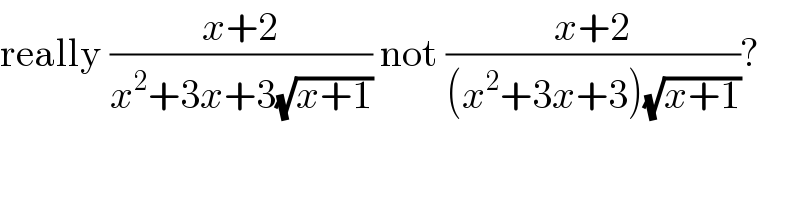
really ((x+2)/(x^2 +3x+3(√(x+1)))) not ((x+2)/((x^2 +3x+3)(√(x+1))))?

$$\mathrm{really}\:\frac{{x}+\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{3}\sqrt{{x}+\mathrm{1}}}\:\mathrm{not}\:\frac{{x}+\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{3}\right)\sqrt{{x}+\mathrm{1}}}? \\ $$

Commented by rajesh4661kumar@gmail.com last updated on 09/Oct/19

$${solve}\:{pleasd} \\ $$

Answered by Kunal12588 last updated on 08/Oct/19

(√(x+1))=t ⇒dt=(1/(2(√(x+1))))dx ⇒dx=2(√(x+1))dt=2tdt x=t^2 −1 I=∫((t^2 +1)/(t^4 −2t^2 +1+3t^2 −3+3t))×2tdt =∫((2t(t^2 +1))/(t^4 +t^2 +3t−2))dt =∫((4t^3 +2t+3−2t^3 −3)/(t^4 +t^2 +3t−2))dt =∫((4t^3 +2t+3)/(t^4 +t^2 +3t−2))dt−∫((2t^3 −3)/(t^4 +t^2 +3t−4))dt =ln∣t^4 +t^2 +3t+4∣−I_2 help from here

$$\sqrt{{x}+\mathrm{1}}={t} \\ $$$$\Rightarrow{dt}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\mathrm{1}}}{dx} \\ $$$$\Rightarrow{dx}=\mathrm{2}\sqrt{{x}+\mathrm{1}}{dt}=\mathrm{2}{tdt} \\ $$$${x}={t}^{\mathrm{2}} −\mathrm{1} \\ $$$${I}=\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}+\mathrm{3}{t}^{\mathrm{2}} −\mathrm{3}+\mathrm{3}{t}}×\mathrm{2}{tdt} \\ $$$$=\int\frac{\mathrm{2}{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{2}}{dt} \\ $$$$=\int\frac{\mathrm{4}{t}^{\mathrm{3}} +\mathrm{2}{t}+\mathrm{3}−\mathrm{2}{t}^{\mathrm{3}} −\mathrm{3}}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{2}}{dt} \\ $$$$=\int\frac{\mathrm{4}{t}^{\mathrm{3}} +\mathrm{2}{t}+\mathrm{3}}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{2}}{dt}−\int\frac{\mathrm{2}{t}^{\mathrm{3}} −\mathrm{3}}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{4}}{dt} \\ $$$$={ln}\mid{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{3}{t}+\mathrm{4}\mid−{I}_{\mathrm{2}} \\ $$$${help}\:{from}\:{here} \\ $$

Commented by MJS last updated on 08/Oct/19

t^4 +t^2 +3t−4=0 has 2 real and 2 complex solutions which are not “nice”. We can only put t^4 +t^2 +3t−4=(t−α)(t−β)(t^2 +γt+δ) and go on decomposing and putting in the approximate values at the end t_1 ≈−1.43546 t_2 ≈.540715 t_(3, 4) ≈.447372±1.54162 α=t_1 β=t_2 γ=−.894744 δ=2.57674

$${t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{4}=\mathrm{0}\:\mathrm{has}\:\mathrm{2}\:\mathrm{real}\:\mathrm{and}\:\mathrm{2}\:\mathrm{complex} \\ $$$$\mathrm{solutions}\:\mathrm{which}\:\mathrm{are}\:\mathrm{not}\:“\mathrm{nice}''.\:\mathrm{We}\:\mathrm{can}\:\mathrm{only} \\ $$$$\mathrm{put}\:{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{4}=\left({t}−\alpha\right)\left({t}−\beta\right)\left({t}^{\mathrm{2}} +\gamma{t}+\delta\right)\:\mathrm{and} \\ $$$$\mathrm{go}\:\mathrm{on}\:\mathrm{decomposing}\:\mathrm{and}\:\mathrm{putting}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{approximate}\:\mathrm{values}\:\mathrm{at}\:\mathrm{the}\:\mathrm{end} \\ $$$${t}_{\mathrm{1}} \approx−\mathrm{1}.\mathrm{43546} \\ $$$${t}_{\mathrm{2}} \approx.\mathrm{540715} \\ $$$${t}_{\mathrm{3},\:\mathrm{4}} \approx.\mathrm{447372}\pm\mathrm{1}.\mathrm{54162} \\ $$$$\alpha={t}_{\mathrm{1}} \\ $$$$\beta={t}_{\mathrm{2}} \\ $$$$\gamma=−.\mathrm{894744} \\ $$$$\delta=\mathrm{2}.\mathrm{57674} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply