Question Number 70808 by rajesh4661kumar@gmail.com last updated on 08/Oct/19
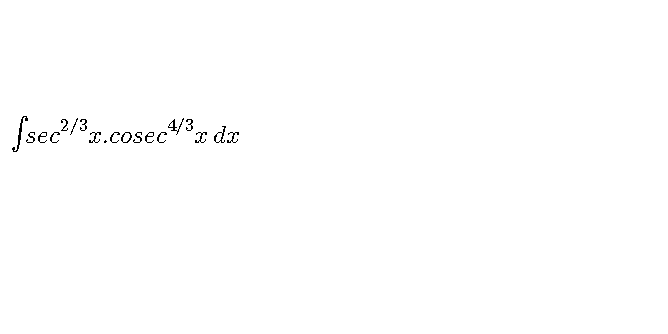
Answered by MJS last updated on 08/Oct/19
![∫(sec x)^(2/3) (csc x)^(4/3) dx=∫(dx/(sin x cos x (tan x)^(1/3) ))= [t=tan x → dx=(cos x)^2 dt] =∫(dt/t^(4/3) )=−(3/t^(1/3) )=−(3/((tan x)^(1/3) ))+C](https://www.tinkutara.com/question/Q70817.png)
$$\int\left(\mathrm{sec}\:{x}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{csc}\:{x}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} {dx}=\int\frac{{dx}}{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\:\left(\mathrm{tan}\:{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\left(\mathrm{cos}\:{x}\right)^{\mathrm{2}} {dt}\right] \\ $$$$=\int\frac{{dt}}{{t}^{\frac{\mathrm{4}}{\mathrm{3}}} }=−\frac{\mathrm{3}}{{t}^{\frac{\mathrm{1}}{\mathrm{3}}} }=−\frac{\mathrm{3}}{\left(\mathrm{tan}\:{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }+{C} \\ $$
