Question-70826

Question Number 70826 by naka3546 last updated on 08/Oct/19

Commented by naka3546 last updated on 08/Oct/19

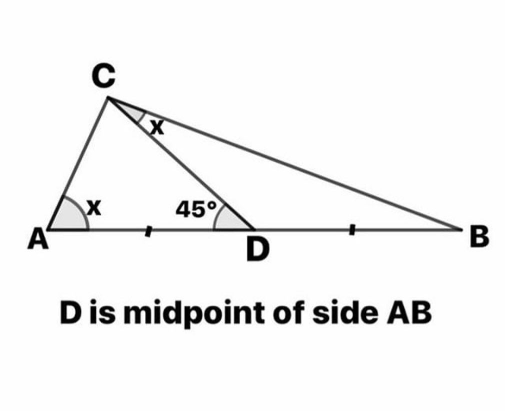
$${Find}\:\:{x}\:. \\ $$

Answered by mind is power last updated on 08/Oct/19

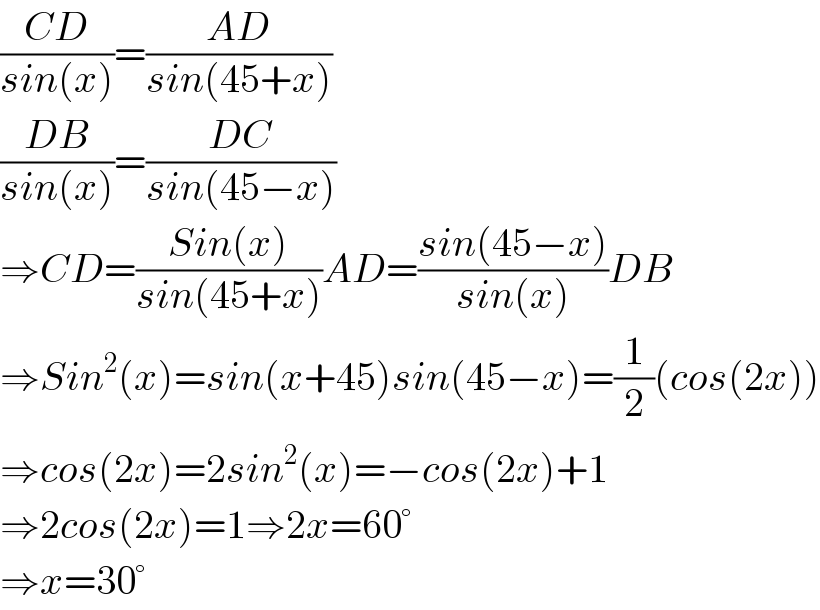
((CD)/(sin(x)))=((AD)/(sin(45+x))) ((DB)/(sin(x)))=((DC)/(sin(45−x))) ⇒CD=((Sin(x))/(sin(45+x)))AD=((sin(45−x))/(sin(x)))DB ⇒Sin^2 (x)=sin(x+45)sin(45−x)=(1/2)(cos(2x)) ⇒cos(2x)=2sin^2 (x)=−cos(2x)+1 ⇒2cos(2x)=1⇒2x=60° ⇒x=30°

$$\frac{{CD}}{{sin}\left({x}\right)}=\frac{{AD}}{{sin}\left(\mathrm{45}+{x}\right)} \\ $$$$\frac{{DB}}{{sin}\left({x}\right)}=\frac{{DC}}{{sin}\left(\mathrm{45}−{x}\right)} \\ $$$$\Rightarrow{CD}=\frac{{Sin}\left({x}\right)}{{sin}\left(\mathrm{45}+{x}\right)}{AD}=\frac{{sin}\left(\mathrm{45}−{x}\right)}{{sin}\left({x}\right)}{DB} \\ $$$$\Rightarrow{Sin}^{\mathrm{2}} \left({x}\right)={sin}\left({x}+\mathrm{45}\right){sin}\left(\mathrm{45}−{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\left(\mathrm{2}{x}\right)\right) \\ $$$$\Rightarrow{cos}\left(\mathrm{2}{x}\right)=\mathrm{2}{sin}^{\mathrm{2}} \left({x}\right)=−{cos}\left(\mathrm{2}{x}\right)+\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}{cos}\left(\mathrm{2}{x}\right)=\mathrm{1}\Rightarrow\mathrm{2}{x}=\mathrm{60}° \\ $$$$\Rightarrow{x}=\mathrm{30}° \\ $$

Commented by naka3546 last updated on 08/Oct/19

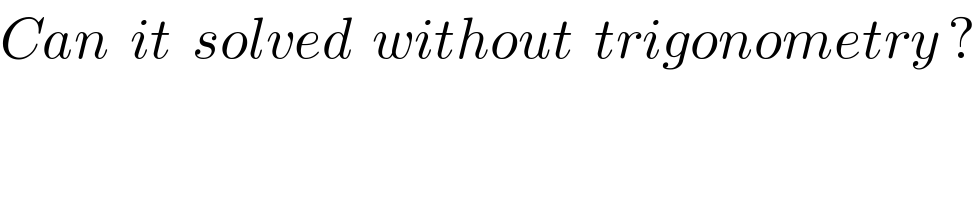
$${Can}\:\:{it}\:\:{solved}\:\:{without}\:\:{trigonometry}\:? \\ $$

Commented by mind is power last updated on 08/Oct/19

$${yes} \\ $$$$ \\ $$

Answered by ajfour last updated on 08/Oct/19

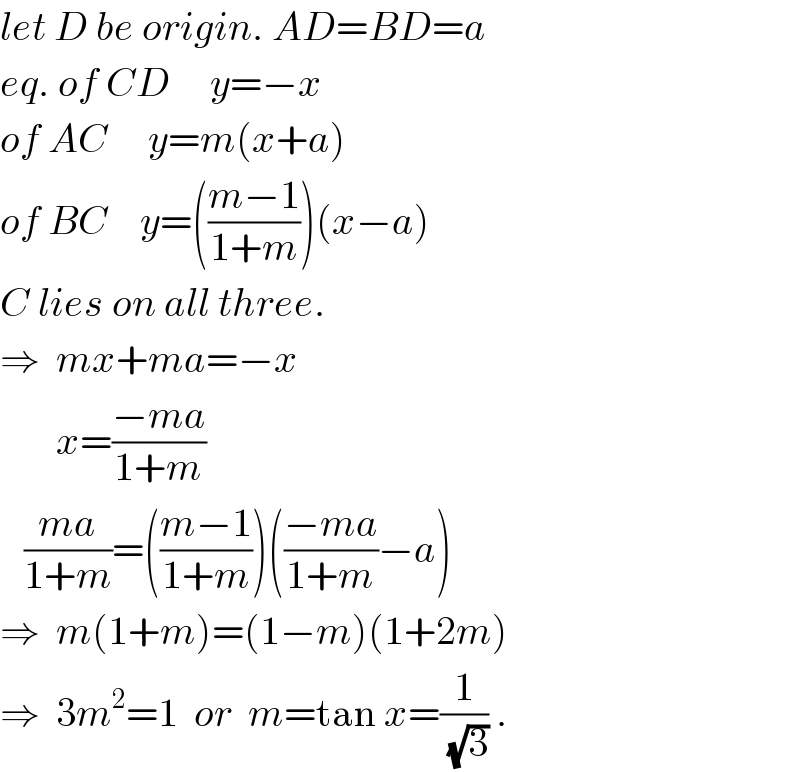
let D be origin. AD=BD=a eq. of CD y=−x of AC y=m(x+a) of BC y=(((m−1)/(1+m)))(x−a) C lies on all three. ⇒ mx+ma=−x x=((−ma)/(1+m)) ((ma)/(1+m))=(((m−1)/(1+m)))(((−ma)/(1+m))−a) ⇒ m(1+m)=(1−m)(1+2m) ⇒ 3m^2 =1 or m=tan x=(1/( (√3))) .

$${let}\:{D}\:{be}\:{origin}.\:{AD}={BD}={a} \\ $$$${eq}.\:{of}\:{CD}\:\:\:\:\:{y}=−{x} \\ $$$${of}\:{AC}\:\:\:\:\:{y}={m}\left({x}+{a}\right) \\ $$$${of}\:{BC}\:\:\:\:{y}=\left(\frac{{m}−\mathrm{1}}{\mathrm{1}+{m}}\right)\left({x}−{a}\right) \\ $$$${C}\:{lies}\:{on}\:{all}\:{three}. \\ $$$$\Rightarrow\:\:{mx}+{ma}=−{x} \\ $$$$\:\:\:\:\:\:\:{x}=\frac{−{ma}}{\mathrm{1}+{m}} \\ $$$$\:\:\:\frac{{ma}}{\mathrm{1}+{m}}=\left(\frac{{m}−\mathrm{1}}{\mathrm{1}+{m}}\right)\left(\frac{−{ma}}{\mathrm{1}+{m}}−{a}\right) \\ $$$$\Rightarrow\:\:{m}\left(\mathrm{1}+{m}\right)=\left(\mathrm{1}−{m}\right)\left(\mathrm{1}+\mathrm{2}{m}\right) \\ $$$$\Rightarrow\:\:\mathrm{3}{m}^{\mathrm{2}} =\mathrm{1}\:\:{or}\:\:{m}=\mathrm{tan}\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply