Question Number 70834 by Maclaurin Stickker last updated on 08/Oct/19
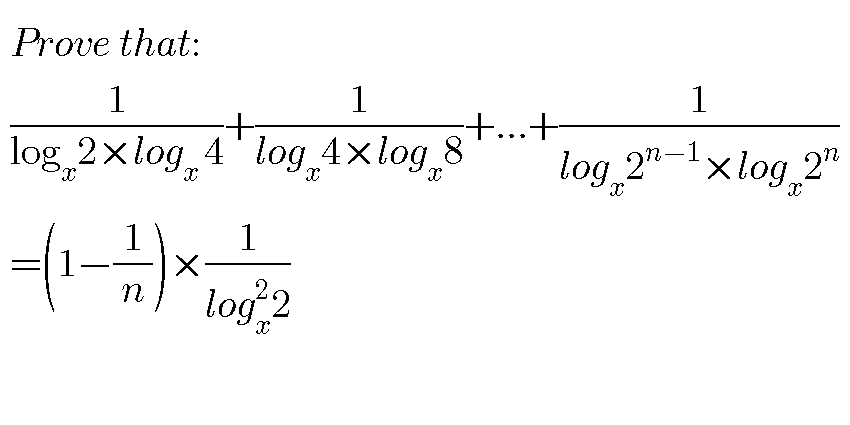
Answered by mind is power last updated on 08/Oct/19
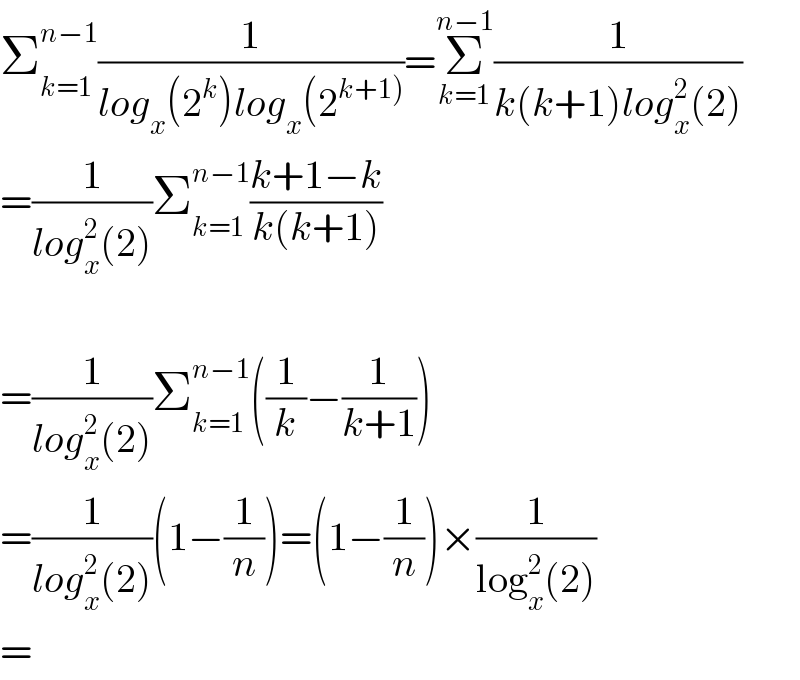
$$\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \frac{\mathrm{1}}{{log}_{{x}} \left(\mathrm{2}^{{k}} \right){log}_{{x}} \left(\mathrm{2}^{\left.{k}+\mathrm{1}\right)} \right.}=\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right){log}_{{x}} ^{\mathrm{2}} \left(\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{{log}_{{x}} ^{\mathrm{2}} \left(\mathrm{2}\right)}\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \frac{{k}+\mathrm{1}−{k}}{{k}\left({k}+\mathrm{1}\right)} \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{{log}_{{x}} ^{\mathrm{2}} \left(\mathrm{2}\right)}\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{{log}_{{x}} ^{\mathrm{2}} \left(\mathrm{2}\right)}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)=\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)×\frac{\mathrm{1}}{\mathrm{log}_{{x}} ^{\mathrm{2}} \left(\mathrm{2}\right)} \\ $$$$= \\ $$
