Question Number 70838 by A8;15: last updated on 08/Oct/19
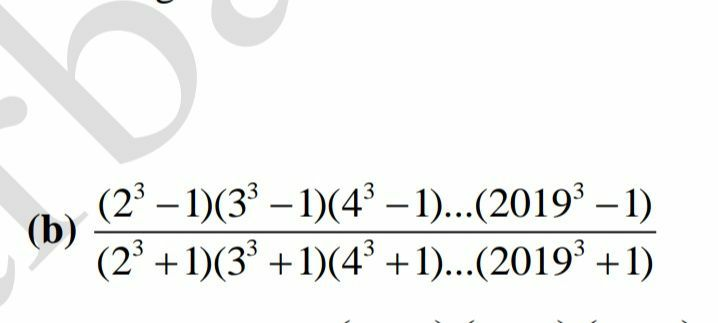
Answered by mind is power last updated on 08/Oct/19
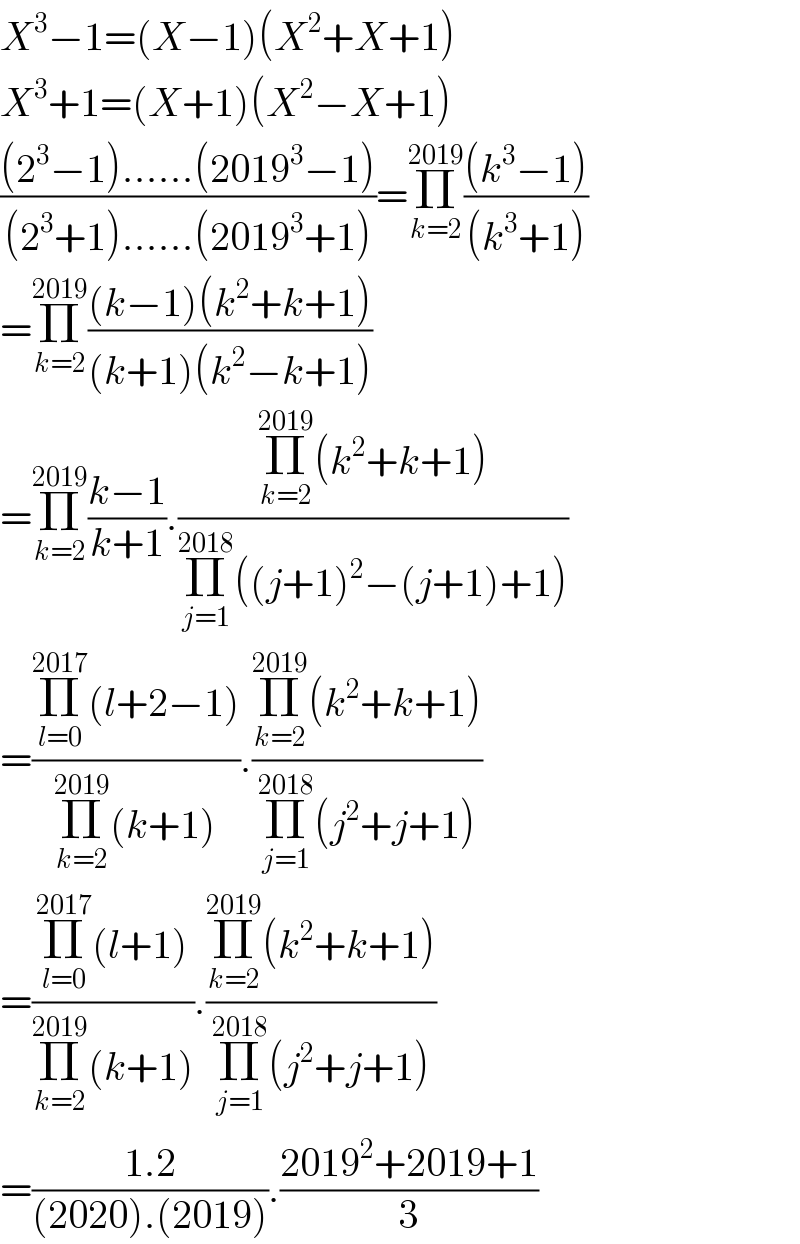
$${X}^{\mathrm{3}} −\mathrm{1}=\left({X}−\mathrm{1}\right)\left({X}^{\mathrm{2}} +{X}+\mathrm{1}\right) \\ $$$${X}^{\mathrm{3}} +\mathrm{1}=\left({X}+\mathrm{1}\right)\left({X}^{\mathrm{2}} −{X}+\mathrm{1}\right) \\ $$$$\frac{\left(\mathrm{2}^{\mathrm{3}} −\mathrm{1}\right)……\left(\mathrm{2019}^{\mathrm{3}} −\mathrm{1}\right)}{\left(\mathrm{2}^{\mathrm{3}} +\mathrm{1}\right)……\left(\mathrm{2019}^{\mathrm{3}} +\mathrm{1}\right)}=\underset{{k}=\mathrm{2}} {\overset{\mathrm{2019}} {\prod}}\frac{\left({k}^{\mathrm{3}} −\mathrm{1}\right)}{\left({k}^{\mathrm{3}} +\mathrm{1}\right)} \\ $$$$=\underset{{k}=\mathrm{2}} {\overset{\mathrm{2019}} {\prod}}\frac{\left({k}−\mathrm{1}\right)\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)}{\left({k}+\mathrm{1}\right)\left({k}^{\mathrm{2}} −{k}+\mathrm{1}\right)} \\ $$$$=\underset{{k}=\mathrm{2}} {\overset{\mathrm{2019}} {\prod}}\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}.\frac{\underset{{k}=\mathrm{2}} {\overset{\mathrm{2019}} {\prod}}\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)}{\underset{{j}=\mathrm{1}} {\overset{\mathrm{2018}} {\prod}}\left(\left({j}+\mathrm{1}\right)^{\mathrm{2}} −\left({j}+\mathrm{1}\right)+\mathrm{1}\right)} \\ $$$$=\frac{\underset{{l}=\mathrm{0}} {\overset{\mathrm{2017}} {\prod}}\left({l}+\mathrm{2}−\mathrm{1}\right)}{\underset{{k}=\mathrm{2}} {\overset{\mathrm{2019}} {\prod}}\left({k}+\mathrm{1}\right)}.\frac{\underset{{k}=\mathrm{2}} {\overset{\mathrm{2019}} {\prod}}\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)}{\underset{{j}=\mathrm{1}} {\overset{\mathrm{2018}} {\prod}}\left({j}^{\mathrm{2}} +{j}+\mathrm{1}\right)} \\ $$$$=\frac{\underset{{l}=\mathrm{0}} {\overset{\mathrm{2017}} {\prod}}\left({l}+\mathrm{1}\right)}{\underset{{k}=\mathrm{2}} {\overset{\mathrm{2019}} {\prod}}\left({k}+\mathrm{1}\right)}.\frac{\underset{{k}=\mathrm{2}} {\overset{\mathrm{2019}} {\prod}}\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)}{\underset{{j}=\mathrm{1}} {\overset{\mathrm{2018}} {\prod}}\left({j}^{\mathrm{2}} +{j}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}.\mathrm{2}}{\left(\mathrm{2020}\right).\left(\mathrm{2019}\right)}.\frac{\mathrm{2019}^{\mathrm{2}} +\mathrm{2019}+\mathrm{1}}{\mathrm{3}} \\ $$
Commented by Prithwish sen last updated on 08/Oct/19

$$\:\mathrm{Beautiful} \\ $$
Commented by mind is power last updated on 08/Oct/19

$${thank}\:{you} \\ $$
Commented by Algoritm last updated on 08/Nov/20

$$. \\ $$
