Question-70996

Question Number 70996 by A8;15: last updated on 10/Oct/19

Commented by mathmax by abdo last updated on 10/Oct/19

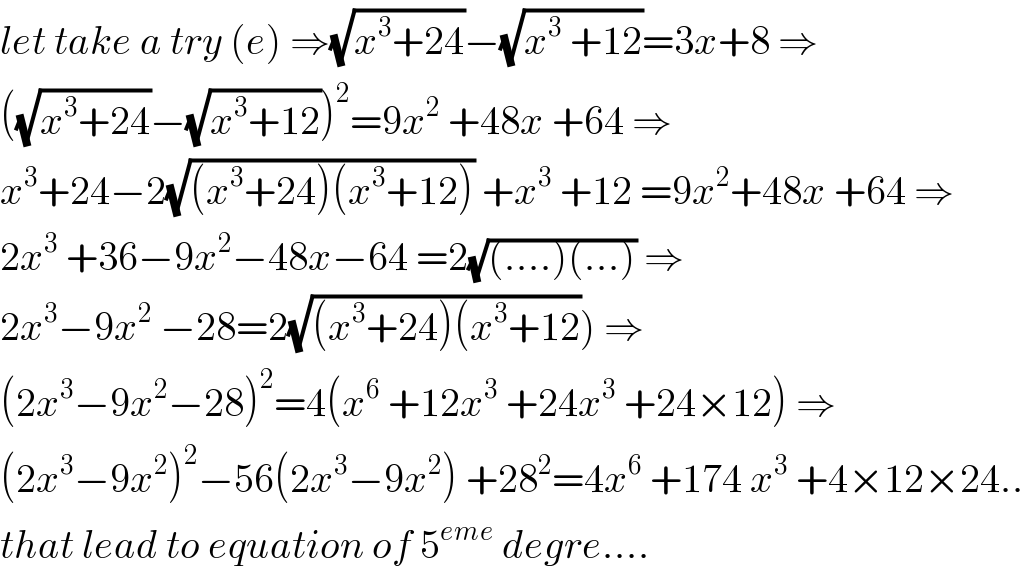
let take a try (e) ⇒(√(x^3 +24))−(√(x^3 +12))=3x+8 ⇒ ((√(x^3 +24))−(√(x^3 +12)))^2 =9x^2 +48x +64 ⇒ x^3 +24−2(√((x^3 +24)(x^3 +12))) +x^3 +12 =9x^2 +48x +64 ⇒ 2x^3 +36−9x^2 −48x−64 =2(√((....)(...))) ⇒ 2x^3 −9x^2 −28=2(√((x^3 +24)(x^3 +12))) ⇒ (2x^3 −9x^2 −28)^2 =4(x^6 +12x^3 +24x^3 +24×12) ⇒ (2x^3 −9x^2 )^2 −56(2x^3 −9x^2 ) +28^2 =4x^6 +174 x^3 +4×12×24.. that lead to equation of 5^(eme) degre....

$${let}\:{take}\:{a}\:{try}\:\left({e}\right)\:\Rightarrow\sqrt{{x}^{\mathrm{3}} +\mathrm{24}}−\sqrt{{x}^{\mathrm{3}} \:+\mathrm{12}}=\mathrm{3}{x}+\mathrm{8}\:\Rightarrow \\ $$$$\left(\sqrt{{x}^{\mathrm{3}} +\mathrm{24}}−\sqrt{{x}^{\mathrm{3}} +\mathrm{12}}\right)^{\mathrm{2}} =\mathrm{9}{x}^{\mathrm{2}} \:+\mathrm{48}{x}\:+\mathrm{64}\:\Rightarrow \\ $$$${x}^{\mathrm{3}} +\mathrm{24}−\mathrm{2}\sqrt{\left({x}^{\mathrm{3}} +\mathrm{24}\right)\left({x}^{\mathrm{3}} +\mathrm{12}\right)}\:+{x}^{\mathrm{3}} \:+\mathrm{12}\:=\mathrm{9}{x}^{\mathrm{2}} +\mathrm{48}{x}\:+\mathrm{64}\:\Rightarrow \\ $$$$\mathrm{2}{x}^{\mathrm{3}} \:+\mathrm{36}−\mathrm{9}{x}^{\mathrm{2}} −\mathrm{48}{x}−\mathrm{64}\:=\mathrm{2}\sqrt{\left(….\right)\left(…\right)}\:\Rightarrow \\ $$$$\left.\mathrm{2}{x}^{\mathrm{3}} −\mathrm{9}{x}^{\mathrm{2}} \:−\mathrm{28}=\mathrm{2}\sqrt{\left({x}^{\mathrm{3}} +\mathrm{24}\right)\left({x}^{\mathrm{3}} +\mathrm{12}\right.}\right)\:\Rightarrow \\ $$$$\left(\mathrm{2}{x}^{\mathrm{3}} −\mathrm{9}{x}^{\mathrm{2}} −\mathrm{28}\right)^{\mathrm{2}} =\mathrm{4}\left({x}^{\mathrm{6}} \:+\mathrm{12}{x}^{\mathrm{3}} \:+\mathrm{24}{x}^{\mathrm{3}} \:+\mathrm{24}×\mathrm{12}\right)\:\Rightarrow \\ $$$$\left(\mathrm{2}{x}^{\mathrm{3}} −\mathrm{9}{x}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{56}\left(\mathrm{2}{x}^{\mathrm{3}} −\mathrm{9}{x}^{\mathrm{2}} \right)\:+\mathrm{28}^{\mathrm{2}} =\mathrm{4}{x}^{\mathrm{6}} \:+\mathrm{174}\:{x}^{\mathrm{3}} \:+\mathrm{4}×\mathrm{12}×\mathrm{24}.. \\ $$$${that}\:{lead}\:{to}\:{equation}\:{of}\:\mathrm{5}^{{eme}} \:{degre}…. \\ $$

Commented by MJS last updated on 10/Oct/19

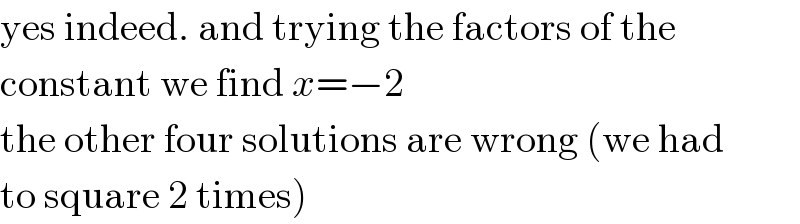
yes indeed. and trying the factors of the constant we find x=−2 the other four solutions are wrong (we had to square 2 times)

$$\mathrm{yes}\:\mathrm{indeed}.\:\mathrm{and}\:\mathrm{trying}\:\mathrm{the}\:\mathrm{factors}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{constant}\:\mathrm{we}\:\mathrm{find}\:{x}=−\mathrm{2} \\ $$$$\mathrm{the}\:\mathrm{other}\:\mathrm{four}\:\mathrm{solutions}\:\mathrm{are}\:\mathrm{wrong}\:\left(\mathrm{we}\:\mathrm{had}\right. \\ $$$$\left.\mathrm{to}\:\mathrm{square}\:\mathrm{2}\:\mathrm{times}\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply