Question-7101

Question Number 7101 by Tawakalitu. last updated on 10/Aug/16

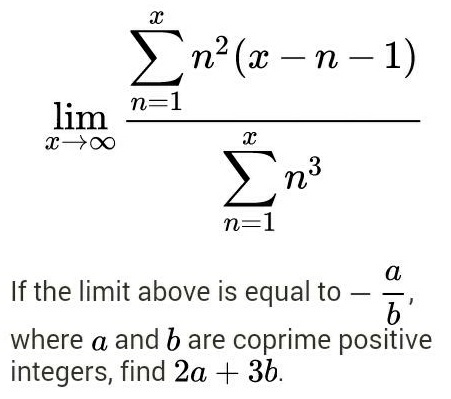
Commented by Tawakalitu. last updated on 10/Aug/16

$${Working}\:{please}\:………… \\ $$

Answered by Yozzii last updated on 10/Aug/16

u(x)=((Σ_(n=1) ^x n^2 (x−n−1))/(Σ_(n=1) ^x n^3 )) (x∈N) [Σ_(n=1) ^x n^3 =((x^2 (x+1)^2 )/4), Σ_(n=1) ^x n^2 =((x(x+1)(2x+1))/6)] u(x)=((Σ_(n=1) ^x {n^2 (x−1)−n^3 })/(x^2 (x+1)^2 /4)) u(x)=(((x−1)((x(x+1)(2x+1))/6)−((x^2 (x+1)^2 )/4))/(x^2 (x+1)^2 /4)) u(x)=((4(x−1)(2x+1))/(6x(x+1)))−1 u(x)=((2(2x^2 −x−1))/(3x^2 +3x))−1 u(x)=((4−2x^(−1) −2x^(−2) )/(3+3x^(−1) ))−1 lim_(x→∞) u(x)=(1/3)??

$${u}\left({x}\right)=\frac{\underset{{n}=\mathrm{1}} {\overset{{x}} {\sum}}{n}^{\mathrm{2}} \left({x}−{n}−\mathrm{1}\right)}{\underset{{n}=\mathrm{1}} {\overset{{x}} {\sum}}{n}^{\mathrm{3}} }\:\:\:\left({x}\in\mathbb{N}\right) \\ $$$$\left[\underset{{n}=\mathrm{1}} {\overset{{x}} {\sum}}{n}^{\mathrm{3}} =\frac{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}},\:\underset{{n}=\mathrm{1}} {\overset{{x}} {\sum}}{n}^{\mathrm{2}} =\frac{{x}\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{6}}\right] \\ $$$${u}\left({x}\right)=\frac{\underset{{n}=\mathrm{1}} {\overset{{x}} {\sum}}\left\{{n}^{\mathrm{2}} \left({x}−\mathrm{1}\right)−{n}^{\mathrm{3}} \right\}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} /\mathrm{4}}\:\: \\ $$$${u}\left({x}\right)=\frac{\left({x}−\mathrm{1}\right)\frac{{x}\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{6}}−\frac{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} /\mathrm{4}} \\ $$$${u}\left({x}\right)=\frac{\mathrm{4}\left({x}−\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{6}{x}\left({x}+\mathrm{1}\right)}−\mathrm{1} \\ $$$${u}\left({x}\right)=\frac{\mathrm{2}\left(\mathrm{2}{x}^{\mathrm{2}} −{x}−\mathrm{1}\right)}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}}−\mathrm{1} \\ $$$${u}\left({x}\right)=\frac{\mathrm{4}−\mathrm{2}{x}^{−\mathrm{1}} −\mathrm{2}{x}^{−\mathrm{2}} }{\mathrm{3}+\mathrm{3}{x}^{−\mathrm{1}} }−\mathrm{1} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}{u}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{3}}?? \\ $$$$ \\ $$$$ \\ $$

Commented by Tawakalitu. last updated on 10/Aug/16