Question Number 71034 by ajfour last updated on 11/Oct/19

Commented by ajfour last updated on 11/Oct/19
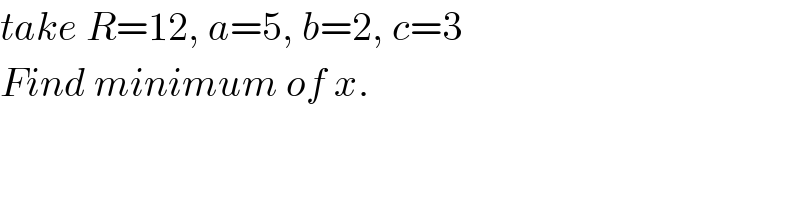
$${take}\:{R}=\mathrm{12},\:{a}=\mathrm{5},\:{b}=\mathrm{2},\:{c}=\mathrm{3} \\ $$$${Find}\:{minimum}\:{of}\:{x}. \\ $$
Commented by ajfour last updated on 11/Oct/19

Commented by ajfour last updated on 11/Oct/19

$${please}\:{solve}..\:\:\left(\underset{\smile} {\overset{\frown} {\bigstar_{\underset{\smile} {\vee}} \bullet}}\right)_{\backslash_{\wedge} } \\ $$
Commented by mr W last updated on 12/Oct/19
![A(0,−(R−a)) B((R−b)cos α,(R−b)sin α) C((R−c)cos β,(R−c)sin β) X(p,q) with radius r (p−0)^2 +[q+(R−a)]^2 =(r+a)^2 ...(i) [p−(R−b)cos α]^2 +[q−(R−b)sin α]^2 =(r+b)^2 ...(ii) [p−(R−c)cos β]^2 +[q−(R−c)sin β]^2 =(r+c)^2 ...(iii) (i)−(ii): (R−b)cos α[2p−(R−b)cos α]+[(R−a)+(R−b)sin α][2q+(R−a)−(R−b)sin α]=(a−b)(2r+a+b) (R−c)cos β[2p−(R−c)cos β]+[(R−a)+(R−c)sin β][2q+(R−a)−(R−c)sin β]=(a−c)(2r+a+c) with A=R−a, B=R−b, C=R−c, P=2p, Q=2q Bcos α[P−Bcos α]+[A+Bsin α][Q+A−Bsin α]=(a−b)(2r+a+b) Ccos β[P−Ccos β]+[A+Csin β][Q+A−Csin β]=(a−c)(2r+a+c) Bcos αP+(A+Bsin α)Q=2(r+R)(B−A) ...(I) Ccos βP+(A+Csin β)Q=2(r+R)(C−A) ...(II) [A(B cos α−C cos β)+BC sin (β−α)]Q=2(r+R)[BC(cos a−cos β)−A(B cos α−C cos β)] ⇒Q=((2(r+R)[BC(cos a−cos β)−A(B cos α−C cos β)])/(A(B cos α−C cos β)+BC sin (β−α))) ⇒q=(r+R)(([BC(cos a−cos β)−A(B cos α−C cos β)])/(A(B cos α−C cos β)+BC sin (β−α))) ⇒q=(r+R)V [A(B cos α−C cos β)+BC sin (β−α)]P=2(r+R)[A(B−C)+BC(sin β−sin α)−A(Csin β−Bsin α)] ⇒P=((2(r+R)[A(B−C)+BC(sin β−sin α)−A(Csin β−Bsin α)])/(A(B cos α−C cos β)+BC sin (β−α))) ⇒p=(r+R)(([A(B−C)+BC(sin β−sin α)−A(Csin β−Bsin α)])/(A(B cos α−C cos β)+BC sin (β−α))) ⇒p=(r+R)U from (i): U^2 (r+R)^2 +[V(r+R)+A]^2 =(r+R−A)^2 let λ=r+R ⇒U^2 λ^2 +(Vλ+A)^2 =(λ−A)^2 ⇒(1−U^2 −V^2 )λ=2A(V+1) ⇒λ=r+R=((2A(V+1))/(1−U^2 −V^2 )) ⇒r=((2A(V+1))/(1−U^2 −V^2 ))−R=f(α,β) with A=R−a B=R−b C=R−c U=((A(B−C)+BC(sin β−sin α)−A(Csin β−Bsin α))/(A(B cos α−C cos β)+BC sin (β−α))) V=((BC(cos a−cos β)−A(B cos α−C cos β))/(A(B cos α−C cos β)+BC sin (β−α))) (∂r/∂α)=0 ⇒ eqn. 1 with α,β (∂r/∂β)=0 ⇒ eqn. 2 with α,β ...](https://www.tinkutara.com/question/Q71100.png)
$${A}\left(\mathrm{0},−\left({R}−{a}\right)\right) \\ $$$${B}\left(\left({R}−{b}\right)\mathrm{cos}\:\alpha,\left({R}−{b}\right)\mathrm{sin}\:\alpha\right) \\ $$$${C}\left(\left({R}−{c}\right)\mathrm{cos}\:\beta,\left({R}−{c}\right)\mathrm{sin}\:\beta\right) \\ $$$${X}\left({p},{q}\right)\:{with}\:{radius}\:{r} \\ $$$$\left({p}−\mathrm{0}\right)^{\mathrm{2}} +\left[{q}+\left({R}−{a}\right)\right]^{\mathrm{2}} =\left({r}+{a}\right)^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$$\left[{p}−\left({R}−{b}\right)\mathrm{cos}\:\alpha\right]^{\mathrm{2}} +\left[{q}−\left({R}−{b}\right)\mathrm{sin}\:\alpha\right]^{\mathrm{2}} =\left({r}+{b}\right)^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$$\left[{p}−\left({R}−{c}\right)\mathrm{cos}\:\beta\right]^{\mathrm{2}} +\left[{q}−\left({R}−{c}\right)\mathrm{sin}\:\beta\right]^{\mathrm{2}} =\left({r}+{c}\right)^{\mathrm{2}} \:\:\:…\left({iii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\left({R}−{b}\right)\mathrm{cos}\:\alpha\left[\mathrm{2}{p}−\left({R}−{b}\right)\mathrm{cos}\:\alpha\right]+\left[\left({R}−{a}\right)+\left({R}−{b}\right)\mathrm{sin}\:\alpha\right]\left[\mathrm{2}{q}+\left({R}−{a}\right)−\left({R}−{b}\right)\mathrm{sin}\:\alpha\right]=\left({a}−{b}\right)\left(\mathrm{2}{r}+{a}+{b}\right) \\ $$$$\left({R}−{c}\right)\mathrm{cos}\:\beta\left[\mathrm{2}{p}−\left({R}−{c}\right)\mathrm{cos}\:\beta\right]+\left[\left({R}−{a}\right)+\left({R}−{c}\right)\mathrm{sin}\:\beta\right]\left[\mathrm{2}{q}+\left({R}−{a}\right)−\left({R}−{c}\right)\mathrm{sin}\:\beta\right]=\left({a}−{c}\right)\left(\mathrm{2}{r}+{a}+{c}\right) \\ $$$${with}\:{A}={R}−{a},\:{B}={R}−{b},\:{C}={R}−{c},\:{P}=\mathrm{2}{p},\:\:{Q}=\mathrm{2}{q} \\ $$$${B}\mathrm{cos}\:\alpha\left[{P}−{B}\mathrm{cos}\:\alpha\right]+\left[{A}+{B}\mathrm{sin}\:\alpha\right]\left[{Q}+{A}−{B}\mathrm{sin}\:\alpha\right]=\left({a}−{b}\right)\left(\mathrm{2}{r}+{a}+{b}\right) \\ $$$${C}\mathrm{cos}\:\beta\left[{P}−{C}\mathrm{cos}\:\beta\right]+\left[{A}+{C}\mathrm{sin}\:\beta\right]\left[{Q}+{A}−{C}\mathrm{sin}\:\beta\right]=\left({a}−{c}\right)\left(\mathrm{2}{r}+{a}+{c}\right) \\ $$$$ \\ $$$${B}\mathrm{cos}\:\alpha{P}+\left({A}+{B}\mathrm{sin}\:\alpha\right){Q}=\mathrm{2}\left({r}+{R}\right)\left({B}−{A}\right)\:\:\:…\left({I}\right) \\ $$$${C}\mathrm{cos}\:\beta{P}+\left({A}+{C}\mathrm{sin}\:\beta\right){Q}=\mathrm{2}\left({r}+{R}\right)\left({C}−{A}\right)\:\:\:…\left({II}\right) \\ $$$$ \\ $$$$\left[{A}\left({B}\:\mathrm{cos}\:\alpha−{C}\:\mathrm{cos}\:\beta\right)+{BC}\:\mathrm{sin}\:\left(\beta−\alpha\right)\right]{Q}=\mathrm{2}\left({r}+{R}\right)\left[{BC}\left(\mathrm{cos}\:{a}−\mathrm{cos}\:\beta\right)−{A}\left({B}\:\mathrm{cos}\:\alpha−{C}\:\mathrm{cos}\:\beta\right)\right] \\ $$$$\Rightarrow{Q}=\frac{\mathrm{2}\left({r}+{R}\right)\left[{BC}\left(\mathrm{cos}\:{a}−\mathrm{cos}\:\beta\right)−{A}\left({B}\:\mathrm{cos}\:\alpha−{C}\:\mathrm{cos}\:\beta\right)\right]}{{A}\left({B}\:\mathrm{cos}\:\alpha−{C}\:\mathrm{cos}\:\beta\right)+{BC}\:\mathrm{sin}\:\left(\beta−\alpha\right)} \\ $$$$\Rightarrow{q}=\left({r}+{R}\right)\frac{\left[{BC}\left(\mathrm{cos}\:{a}−\mathrm{cos}\:\beta\right)−{A}\left({B}\:\mathrm{cos}\:\alpha−{C}\:\mathrm{cos}\:\beta\right)\right]}{{A}\left({B}\:\mathrm{cos}\:\alpha−{C}\:\mathrm{cos}\:\beta\right)+{BC}\:\mathrm{sin}\:\left(\beta−\alpha\right)} \\ $$$$\Rightarrow{q}=\left({r}+{R}\right){V} \\ $$$$\left[{A}\left({B}\:\mathrm{cos}\:\alpha−{C}\:\mathrm{cos}\:\beta\right)+{BC}\:\mathrm{sin}\:\left(\beta−\alpha\right)\right]{P}=\mathrm{2}\left({r}+{R}\right)\left[{A}\left({B}−{C}\right)+{BC}\left(\mathrm{sin}\:\beta−\mathrm{sin}\:\alpha\right)−{A}\left({C}\mathrm{sin}\:\beta−{B}\mathrm{sin}\:\alpha\right)\right] \\ $$$$\Rightarrow{P}=\frac{\mathrm{2}\left({r}+{R}\right)\left[{A}\left({B}−{C}\right)+{BC}\left(\mathrm{sin}\:\beta−\mathrm{sin}\:\alpha\right)−{A}\left({C}\mathrm{sin}\:\beta−{B}\mathrm{sin}\:\alpha\right)\right]}{{A}\left({B}\:\mathrm{cos}\:\alpha−{C}\:\mathrm{cos}\:\beta\right)+{BC}\:\mathrm{sin}\:\left(\beta−\alpha\right)}\: \\ $$$$\Rightarrow{p}=\left({r}+{R}\right)\frac{\left[{A}\left({B}−{C}\right)+{BC}\left(\mathrm{sin}\:\beta−\mathrm{sin}\:\alpha\right)−{A}\left({C}\mathrm{sin}\:\beta−{B}\mathrm{sin}\:\alpha\right)\right]}{{A}\left({B}\:\mathrm{cos}\:\alpha−{C}\:\mathrm{cos}\:\beta\right)+{BC}\:\mathrm{sin}\:\left(\beta−\alpha\right)}\: \\ $$$$\Rightarrow{p}=\left({r}+{R}\right){U}\: \\ $$$${from}\:\left({i}\right): \\ $$$${U}^{\mathrm{2}} \left({r}+{R}\right)^{\mathrm{2}} +\left[{V}\left({r}+{R}\right)+{A}\right]^{\mathrm{2}} =\left({r}+{R}−{A}\right)^{\mathrm{2}} \:\:\: \\ $$$${let}\:\lambda={r}+{R} \\ $$$$\Rightarrow{U}^{\mathrm{2}} \lambda^{\mathrm{2}} +\left({V}\lambda+{A}\right)^{\mathrm{2}} =\left(\lambda−{A}\right)^{\mathrm{2}} \:\:\: \\ $$$$\Rightarrow\left(\mathrm{1}−{U}^{\mathrm{2}} −{V}^{\mathrm{2}} \right)\lambda=\mathrm{2}{A}\left({V}+\mathrm{1}\right)\:\: \\ $$$$\Rightarrow\lambda={r}+{R}=\frac{\mathrm{2}{A}\left({V}+\mathrm{1}\right)}{\mathrm{1}−{U}^{\mathrm{2}} −{V}^{\mathrm{2}} } \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}{A}\left({V}+\mathrm{1}\right)}{\mathrm{1}−{U}^{\mathrm{2}} −{V}^{\mathrm{2}} }−{R}={f}\left(\alpha,\beta\right) \\ $$$${with} \\ $$$${A}={R}−{a} \\ $$$${B}={R}−{b} \\ $$$${C}={R}−{c} \\ $$$${U}=\frac{{A}\left({B}−{C}\right)+{BC}\left(\mathrm{sin}\:\beta−\mathrm{sin}\:\alpha\right)−{A}\left({C}\mathrm{sin}\:\beta−{B}\mathrm{sin}\:\alpha\right)}{{A}\left({B}\:\mathrm{cos}\:\alpha−{C}\:\mathrm{cos}\:\beta\right)+{BC}\:\mathrm{sin}\:\left(\beta−\alpha\right)}\: \\ $$$${V}=\frac{{BC}\left(\mathrm{cos}\:{a}−\mathrm{cos}\:\beta\right)−{A}\left({B}\:\mathrm{cos}\:\alpha−{C}\:\mathrm{cos}\:\beta\right)}{{A}\left({B}\:\mathrm{cos}\:\alpha−{C}\:\mathrm{cos}\:\beta\right)+{BC}\:\mathrm{sin}\:\left(\beta−\alpha\right)} \\ $$$$\frac{\partial{r}}{\partial\alpha}=\mathrm{0}\:\Rightarrow\:{eqn}.\:\mathrm{1}\:{with}\:\alpha,\beta \\ $$$$\frac{\partial{r}}{\partial\beta}=\mathrm{0}\:\Rightarrow\:{eqn}.\:\mathrm{2}\:{with}\:\alpha,\beta \\ $$$$… \\ $$
Commented by peter frank last updated on 11/Oct/19
$${please}\:{sir}\:{help}\: \\ $$$${Qn}\:\mathrm{69230},\mathrm{70562} \\ $$
Commented by ajfour last updated on 12/Oct/19
$${thank}\:{you}\:{sir},\:{let}\:{me}\:{try}\:{a}\:{bit} \\ $$$${off}\:{route}.. \\ $$
