Question-71054

Question Number 71054 by jagannath19 last updated on 11/Oct/19

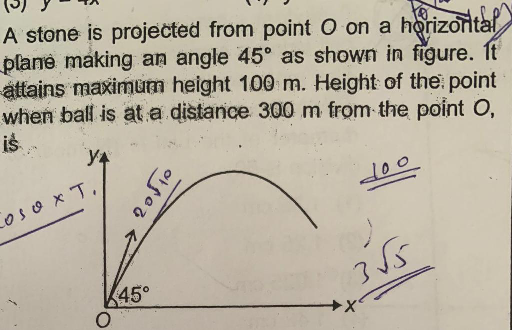
Commented by jagannath19 last updated on 11/Oct/19

$${with}\:{explanation} \\ $$

Commented by mr W last updated on 11/Oct/19

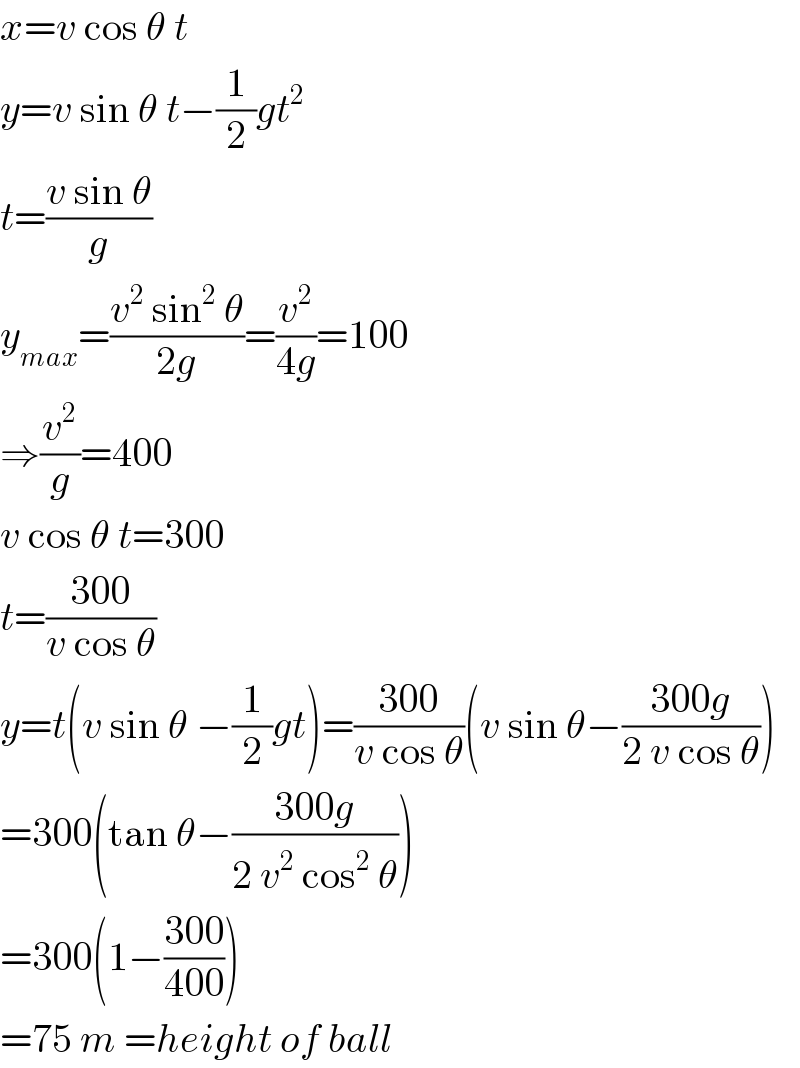
x=v cos θ t y=v sin θ t−(1/2)gt^2 t=((v sin θ)/g) y_(max) =((v^2 sin^2 θ)/(2g))=(v^2 /(4g))=100 ⇒(v^2 /g)=400 v cos θ t=300 t=((300)/(v cos θ)) y=t(v sin θ −(1/2)gt)=((300)/(v cos θ))(v sin θ−((300g)/(2 v cos θ))) =300(tan θ−((300g)/(2 v^2 cos^2 θ))) =300(1−((300)/(400))) =75 m =height of ball

$${x}={v}\:\mathrm{cos}\:\theta\:{t} \\ $$$${y}={v}\:\mathrm{sin}\:\theta\:{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$${t}=\frac{{v}\:\mathrm{sin}\:\theta}{{g}} \\ $$$${y}_{{max}} =\frac{{v}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{2}{g}}=\frac{{v}^{\mathrm{2}} }{\mathrm{4}{g}}=\mathrm{100} \\ $$$$\Rightarrow\frac{{v}^{\mathrm{2}} }{{g}}=\mathrm{400} \\ $$$${v}\:\mathrm{cos}\:\theta\:{t}=\mathrm{300} \\ $$$${t}=\frac{\mathrm{300}}{{v}\:\mathrm{cos}\:\theta} \\ $$$${y}={t}\left({v}\:\mathrm{sin}\:\theta\:−\frac{\mathrm{1}}{\mathrm{2}}{gt}\right)=\frac{\mathrm{300}}{{v}\:\mathrm{cos}\:\theta}\left({v}\:\mathrm{sin}\:\theta−\frac{\mathrm{300}{g}}{\mathrm{2}\:{v}\:\mathrm{cos}\:\theta}\right) \\ $$$$=\mathrm{300}\left(\mathrm{tan}\:\theta−\frac{\mathrm{300}{g}}{\mathrm{2}\:{v}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta}\right) \\ $$$$=\mathrm{300}\left(\mathrm{1}−\frac{\mathrm{300}}{\mathrm{400}}\right) \\ $$$$=\mathrm{75}\:{m}\:={height}\:{of}\:{ball} \\ $$

Facebook Tweet Pin

Question-71054

Leave a Reply Cancel reply