Question Number 71073 by TawaTawa last updated on 11/Oct/19
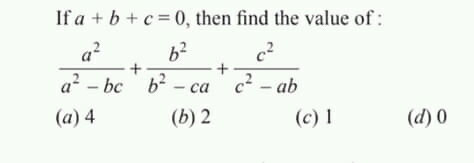
Commented by Prithwish sen last updated on 11/Oct/19

$$\mathrm{a}^{\mathrm{2}} =\:\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} +\mathrm{2bc} \\ $$$$\therefore\:\boldsymbol{\mathrm{bc}}\:=\:\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{c}}^{\mathrm{2}} }{\mathrm{2}}\Rightarrow\:\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\boldsymbol{\mathrm{bc}}\:=\:\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\boldsymbol{\mathrm{c}}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{Similarly}}\:\:\:\:\:\:\:\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{ca}}\:=\:\:\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\boldsymbol{\mathrm{c}}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{c}}^{\mathrm{2}} −\boldsymbol{\mathrm{ab}}\:=\:\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\boldsymbol{\mathrm{c}}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\therefore\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{expression}} \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} }{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\boldsymbol{\mathrm{c}}^{\mathrm{2}} }\:+\frac{\mathrm{2}\boldsymbol{\mathrm{b}}^{\mathrm{2}} }{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\boldsymbol{\mathrm{c}}^{\mathrm{2}} }+\frac{\mathrm{2}\boldsymbol{\mathrm{c}}^{\mathrm{2}} }{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\boldsymbol{\mathrm{c}}^{\mathrm{2}} }\:=\:\mathrm{2} \\ $$
Commented by Henri Boucatchou last updated on 11/Oct/19

$$\boldsymbol{{Nice}}… \\ $$
Commented by Prithwish sen last updated on 11/Oct/19

$$\boldsymbol{\mathrm{Thank}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{Sir}}. \\ $$
Commented by TawaTawa last updated on 11/Oct/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by $@ty@m123 last updated on 11/Oct/19

$${Following}\:{method}\:{can}\:{be}\:{used} \\ $$$${to}\:{find}\:{quick}\:{solution}\:{of}\:{MCQ}: \\ $$$${Let}\:{a}=−\mathrm{1},\:{b}=\mathrm{0},{c}=\mathrm{1} \\ $$$$\therefore\:{Given}\:{expression}: \\ $$$$\mathrm{1}+\mathrm{0}+\mathrm{1}=\mathrm{2} \\ $$
Commented by MJS last updated on 11/Oct/19

$$\mathrm{but}\:\mathrm{then}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{valid}\:\mathrm{for}\:\mathrm{all}\:\mathrm{values}\:\mathrm{of}\:{a},\:{b},\:{c} \\ $$$$\mathrm{with}\:{a}+{b}+{c}=\mathrm{0} \\ $$
Commented by $@ty@m123 last updated on 11/Oct/19

$${Can}\:{you}\:{give}\:{an}\:{example}? \\ $$
Commented by $@ty@m123 last updated on 11/Oct/19

$${Of}\:{course}, \\ $$$${this}\:{is}\:{not}\:{a}\:{proper}\:\left({traditional}\right) \\ $$$${way},\:{but}\:{in}\:{MCQ}\:{type}\:{tests},\:{we}\:{need}\:{tricky} \\ $$$${approach}\:{to}\:{save}\:{time}. \\ $$$$ \\ $$
Answered by MJS last updated on 11/Oct/19

$${c}=−\left({a}+{b}\right) \\ $$$$\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} }+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} }+\frac{\left({a}+{b}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} }=\mathrm{2} \\ $$$$ \\ $$
Commented by Prithwish sen last updated on 11/Oct/19

$$<\boldsymbol{\mathrm{Excellent}}\:\boldsymbol{\mathrm{Sir}}\:! \\ $$
Commented by MJS last updated on 11/Oct/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by TawaTawa last updated on 11/Oct/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by peter frank last updated on 11/Oct/19

$${a}+{b}+{c}=\mathrm{0} \\ $$$${a}=−{b}−{c} \\ $$$${a}^{\mathrm{2}} =−{ab}−{ac}….\left({i}\right) \\ $$$${a}+{b}+{c}=\mathrm{0} \\ $$$${b}=−{a}−{c} \\ $$$${b}^{\mathrm{2}} =−{ab}−{cb}….\left({ii}\right) \\ $$$${a}+{b}+{c}=\mathrm{0} \\ $$$${c}=−{a}−{b} \\ $$$${c}^{\mathrm{2}} =−{ac}−{bc}…..\left({iii}\right) \\ $$$${from} \\ $$$$\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{bc}}+\frac{{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} −{ca}}+\frac{{c}^{\mathrm{2}} }{{c}^{\mathrm{2}} −{ab}}….\left({iv}\right) \\ $$$${substitutes}\:{i}\:{ii}\:{iii}\:{in}\:{iv} \\ $$$${a}^{\mathrm{2}} =−{ab}−{ac}….\left({i}\right) \\ $$$${b}^{\mathrm{2}} =−{ab}−{cb}….\left({ii}\right) \\ $$$${c}^{\mathrm{2}} =−{ac}−{bc}…..\left({iii}\right) \\ $$$$\frac{{ab}+{ca}}{{ab}+{ca}+{bc}}+\frac{{ba}+{bc}}{{ab}+{ca}+{bc}}+\frac{{ca}+{cb}}{{ab}+{ca}+{bc}} \\ $$$$\frac{\mathrm{2}{ab}+\mathrm{2}{ac}+\mathrm{2}{bc}}{{ab}+{ca}+{bc}} \\ $$$$\mathrm{2} \\ $$$$ \\ $$
Commented by TawaTawa last updated on 11/Oct/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
