Question Number 71096 by Omer Alattas last updated on 11/Oct/19
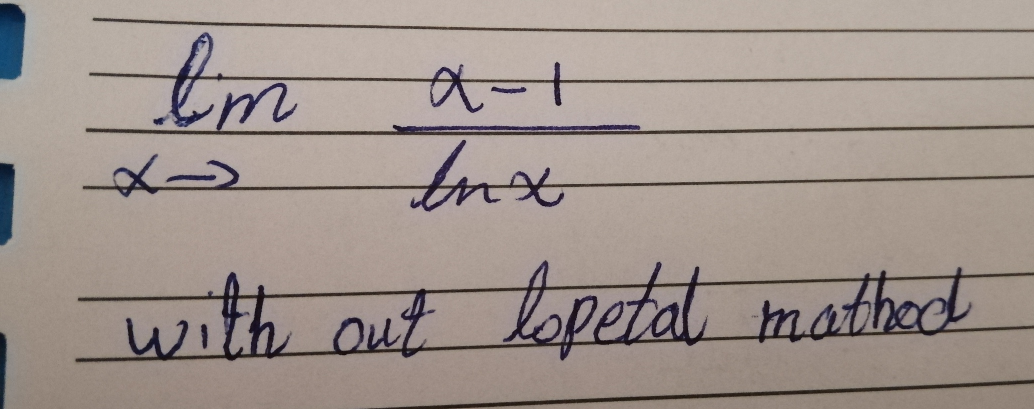
Answered by $@ty@m123 last updated on 11/Oct/19
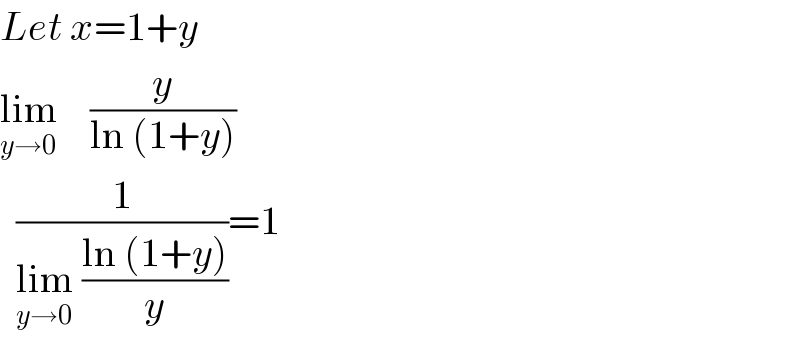
$${Let}\:{x}=\mathrm{1}+{y} \\ $$$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{{y}}{\mathrm{ln}\:\left(\mathrm{1}+{y}\right)} \\ $$$$\:\:\frac{\mathrm{1}}{\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\mathrm{1}+{y}\right)}{{y}}}=\mathrm{1} \\ $$
Commented by Omer Alattas last updated on 11/Oct/19
$${thank}\:{you}\:{very}\:{much} \\ $$
Commented by $@ty@m123 last updated on 11/Oct/19
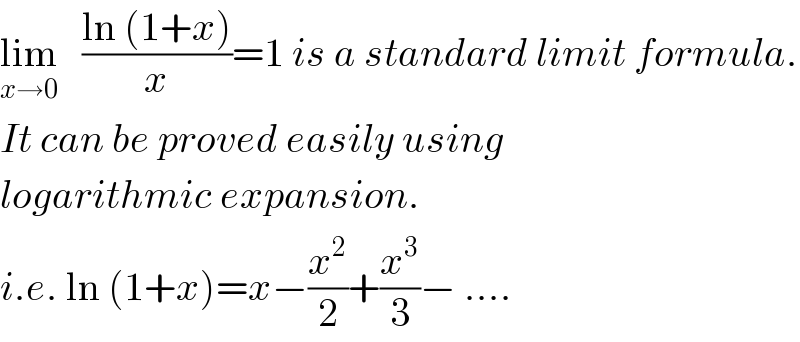
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\mathrm{ln}\:\left(\mathrm{1}+{x}\right)}{{x}}=\mathrm{1}\:{is}\:{a}\:{standard}\:{limit}\:{formula}. \\ $$$${It}\:{can}\:{be}\:{proved}\:{easily}\:{using} \\ $$$${logarithmic}\:{expansion}. \\ $$$${i}.{e}.\:\mathrm{ln}\:\left(\mathrm{1}+{x}\right)={x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\:…. \\ $$
Commented by malwaan last updated on 11/Oct/19
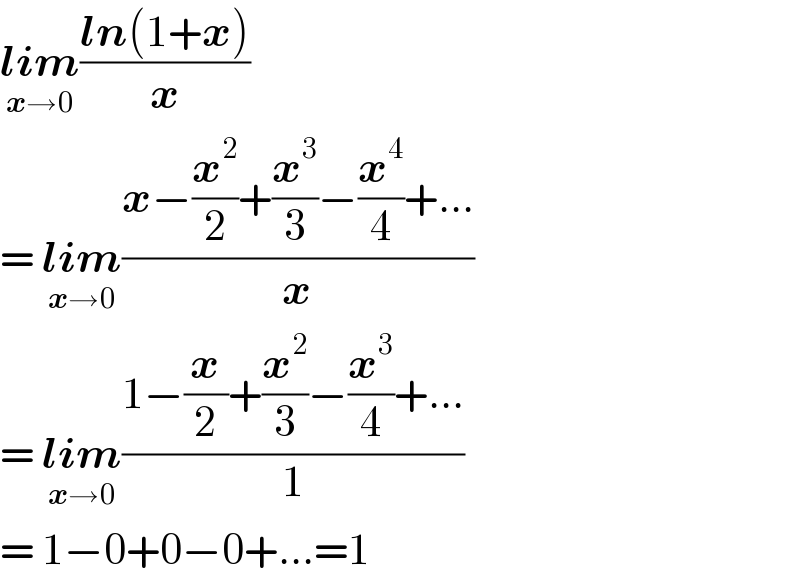
$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\frac{\boldsymbol{{ln}}\left(\mathrm{1}+\boldsymbol{{x}}\right)}{\boldsymbol{{x}}} \\ $$$$=\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\frac{\boldsymbol{{x}}−\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{2}}+\frac{\boldsymbol{{x}}^{\mathrm{3}} }{\mathrm{3}}−\frac{\boldsymbol{{x}}^{\mathrm{4}} }{\mathrm{4}}+…}{\boldsymbol{{x}}} \\ $$$$=\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\frac{\mathrm{1}−\frac{\boldsymbol{{x}}}{\mathrm{2}}+\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{3}}−\frac{\boldsymbol{{x}}^{\mathrm{3}} }{\mathrm{4}}+…}{\mathrm{1}} \\ $$$$=\:\mathrm{1}−\mathrm{0}+\mathrm{0}−\mathrm{0}+…=\mathrm{1} \\ $$
