Question-71147

Question Number 71147 by mr W last updated on 12/Oct/19

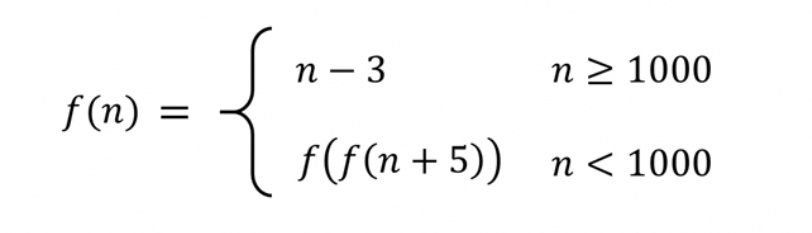
Commented by mr W last updated on 12/Oct/19

$${find}\:{f}\left(\mathrm{5}\right)=? \\ $$

Answered by MJS last updated on 12/Oct/19

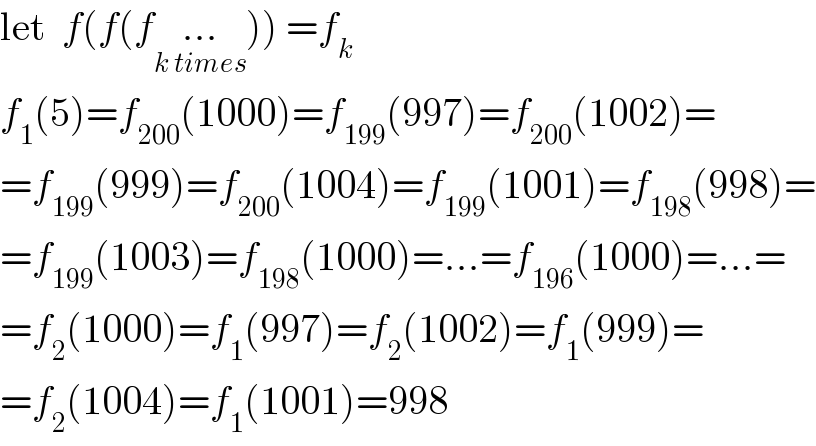
let f(f(f..._(k times) )) =f_k f_1 (5)=f_(200) (1000)=f_(199) (997)=f_(200) (1002)= =f_(199) (999)=f_(200) (1004)=f_(199) (1001)=f_(198) (998)= =f_(199) (1003)=f_(198) (1000)=...=f_(196) (1000)=...= =f_2 (1000)=f_1 (997)=f_2 (1002)=f_1 (999)= =f_2 (1004)=f_1 (1001)=998

$$\mathrm{let}\:\:{f}\left({f}\left({f}\underset{{k}\:{times}} {…}\right)\right)\:={f}_{{k}} \\ $$$${f}_{\mathrm{1}} \left(\mathrm{5}\right)={f}_{\mathrm{200}} \left(\mathrm{1000}\right)={f}_{\mathrm{199}} \left(\mathrm{997}\right)={f}_{\mathrm{200}} \left(\mathrm{1002}\right)= \\ $$$$={f}_{\mathrm{199}} \left(\mathrm{999}\right)={f}_{\mathrm{200}} \left(\mathrm{1004}\right)={f}_{\mathrm{199}} \left(\mathrm{1001}\right)={f}_{\mathrm{198}} \left(\mathrm{998}\right)= \\ $$$$={f}_{\mathrm{199}} \left(\mathrm{1003}\right)={f}_{\mathrm{198}} \left(\mathrm{1000}\right)=…={f}_{\mathrm{196}} \left(\mathrm{1000}\right)=…= \\ $$$$={f}_{\mathrm{2}} \left(\mathrm{1000}\right)={f}_{\mathrm{1}} \left(\mathrm{997}\right)={f}_{\mathrm{2}} \left(\mathrm{1002}\right)={f}_{\mathrm{1}} \left(\mathrm{999}\right)= \\ $$$$={f}_{\mathrm{2}} \left(\mathrm{1004}\right)={f}_{\mathrm{1}} \left(\mathrm{1001}\right)=\mathrm{998} \\ $$

Commented by mr W last updated on 12/Oct/19

$${thanks}! \\ $$

Commented by mr W last updated on 12/Oct/19

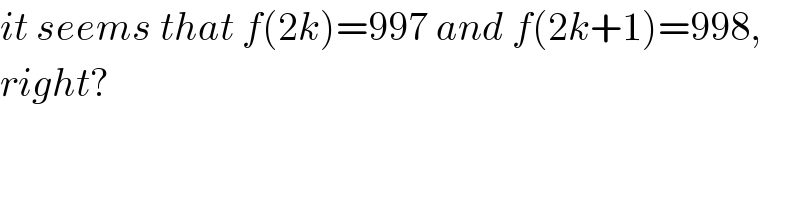
it seems that f(2k)=997 and f(2k+1)=998, right?

$${it}\:{seems}\:{that}\:{f}\left(\mathrm{2}{k}\right)=\mathrm{997}\:{and}\:{f}\left(\mathrm{2}{k}+\mathrm{1}\right)=\mathrm{998}, \\ $$$${right}? \\ $$

Answered by mind is power last updated on 12/Oct/19

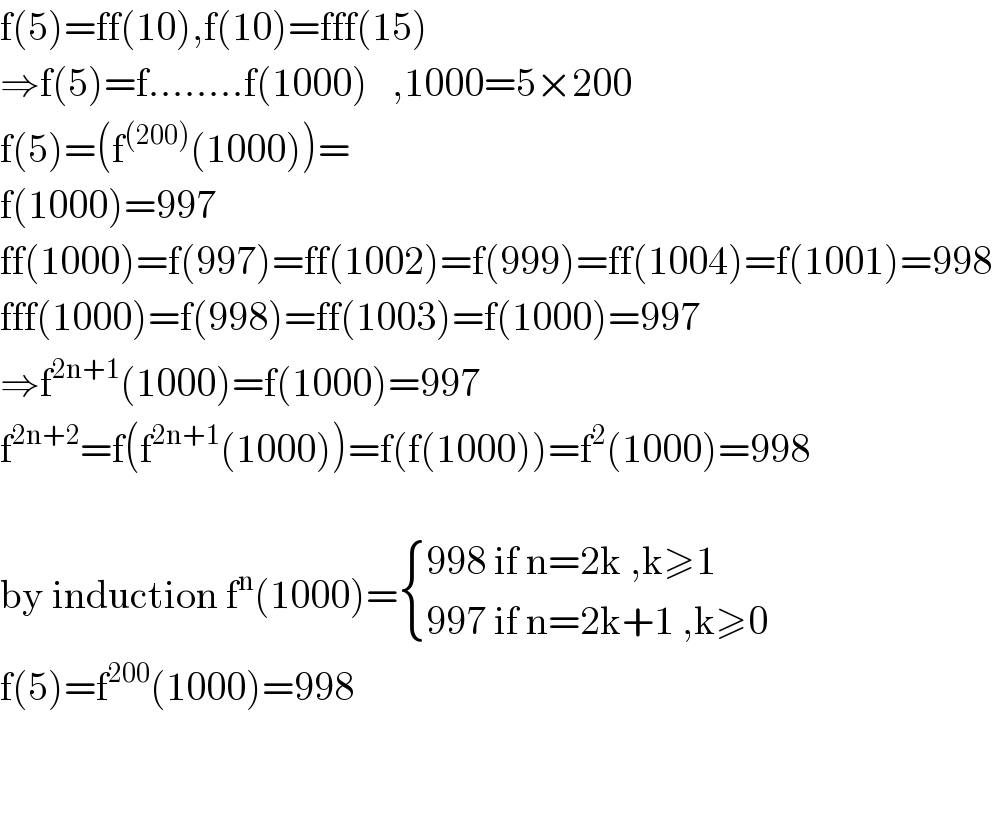
f(5)=ff(10),f(10)=fff(15) ⇒f(5)=f........f(1000) ,1000=5×200 f(5)=(f^((200)) (1000))= f(1000)=997 ff(1000)=f(997)=ff(1002)=f(999)=ff(1004)=f(1001)=998 fff(1000)=f(998)=ff(1003)=f(1000)=997 ⇒f^(2n+1) (1000)=f(1000)=997 f^(2n+2) =f(f^(2n+1) (1000))=f(f(1000))=f^2 (1000)=998 by induction f^n (1000)= { ((998 if n=2k ,k≥1)),((997 if n=2k+1 ,k≥0)) :} f(5)=f^(200) (1000)=998

$$\mathrm{f}\left(\mathrm{5}\right)=\mathrm{ff}\left(\mathrm{10}\right),\mathrm{f}\left(\mathrm{10}\right)=\mathrm{fff}\left(\mathrm{15}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{5}\right)=\mathrm{f}……..\mathrm{f}\left(\mathrm{1000}\right)\:\:\:,\mathrm{1000}=\mathrm{5}×\mathrm{200} \\ $$$$\mathrm{f}\left(\mathrm{5}\right)=\left(\mathrm{f}^{\left(\mathrm{200}\right)} \left(\mathrm{1000}\right)\right)= \\ $$$$\mathrm{f}\left(\mathrm{1000}\right)=\mathrm{997} \\ $$$$\mathrm{ff}\left(\mathrm{1000}\right)=\mathrm{f}\left(\mathrm{997}\right)=\mathrm{ff}\left(\mathrm{1002}\right)=\mathrm{f}\left(\mathrm{999}\right)=\mathrm{ff}\left(\mathrm{1004}\right)=\mathrm{f}\left(\mathrm{1001}\right)=\mathrm{998} \\ $$$$\mathrm{fff}\left(\mathrm{1000}\right)=\mathrm{f}\left(\mathrm{998}\right)=\mathrm{ff}\left(\mathrm{1003}\right)=\mathrm{f}\left(\mathrm{1000}\right)=\mathrm{997} \\ $$$$\Rightarrow\mathrm{f}^{\mathrm{2n}+\mathrm{1}} \left(\mathrm{1000}\right)=\mathrm{f}\left(\mathrm{1000}\right)=\mathrm{997} \\ $$$$\mathrm{f}^{\mathrm{2n}+\mathrm{2}} =\mathrm{f}\left(\mathrm{f}^{\mathrm{2n}+\mathrm{1}} \left(\mathrm{1000}\right)\right)=\mathrm{f}\left(\mathrm{f}\left(\mathrm{1000}\right)\right)=\mathrm{f}^{\mathrm{2}} \left(\mathrm{1000}\right)=\mathrm{998} \\ $$$$ \\ $$$$\mathrm{by}\:\mathrm{induction}\:\mathrm{f}^{\mathrm{n}} \left(\mathrm{1000}\right)=\begin{cases}{\mathrm{998}\:\mathrm{if}\:\mathrm{n}=\mathrm{2k}\:,\mathrm{k}\geqslant\mathrm{1}}\\{\mathrm{997}\:\mathrm{if}\:\mathrm{n}=\mathrm{2k}+\mathrm{1}\:,\mathrm{k}\geqslant\mathrm{0}}\end{cases} \\ $$$$\mathrm{f}\left(\mathrm{5}\right)=\mathrm{f}^{\mathrm{200}} \left(\mathrm{1000}\right)=\mathrm{998} \\ $$$$ \\ $$$$ \\ $$

Commented by mr W last updated on 12/Oct/19

$${thanks}! \\ $$

Commented by mind is power last updated on 12/Oct/19

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply