Question Number 71149 by naka3546 last updated on 12/Oct/19

Commented by MJS last updated on 17/Oct/19
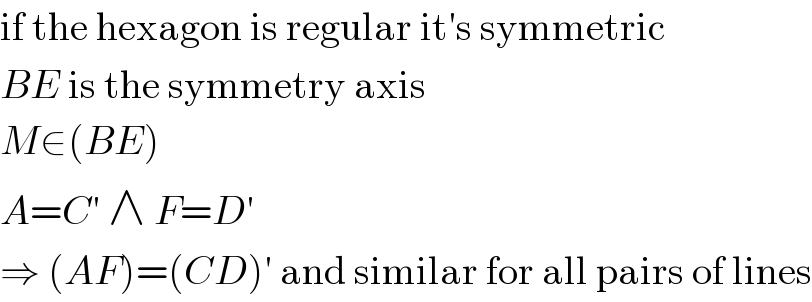
$$\mathrm{if}\:\mathrm{the}\:\mathrm{hexagon}\:\mathrm{is}\:\mathrm{regular}\:\mathrm{it}'\mathrm{s}\:\mathrm{symmetric} \\ $$$${BE}\:\mathrm{is}\:\mathrm{the}\:\mathrm{symmetry}\:\mathrm{axis} \\ $$$${M}\in\left({BE}\right) \\ $$$${A}={C}'\:\wedge\:{F}={D}' \\ $$$$\Rightarrow\:\left({AF}\right)=\left({CD}\right)'\:\mathrm{and}\:\mathrm{similar}\:\mathrm{for}\:\mathrm{all}\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{lines} \\ $$
Commented by naka3546 last updated on 12/Oct/19
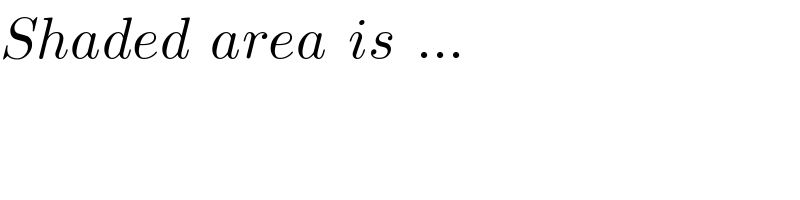
$${Shaded}\:\:{area}\:\:{is}\:\:… \\ $$
Commented by MJS last updated on 13/Oct/19
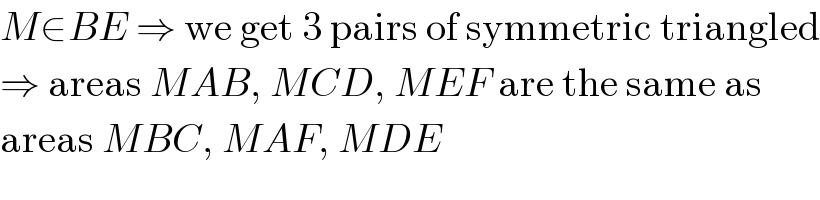
$${M}\in{BE}\:\Rightarrow\:\mathrm{we}\:\mathrm{get}\:\mathrm{3}\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{symmetric}\:\mathrm{triangled} \\ $$$$\Rightarrow\:\mathrm{areas}\:{MAB},\:{MCD},\:{MEF}\:\mathrm{are}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as} \\ $$$$\mathrm{areas}\:{MBC},\:{MAF},\:{MDE} \\ $$
Commented by naka3546 last updated on 14/Oct/19

$${how}\:\:{to}\:\:{prove}\:\:{them}\:\:{are}\:\:{symmetric}\:\:{triangled}\:\:? \\ $$
Answered by MJS last updated on 12/Oct/19
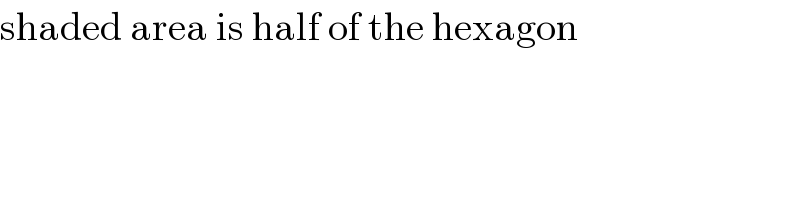
$$\mathrm{shaded}\:\mathrm{area}\:\mathrm{is}\:\mathrm{half}\:\mathrm{of}\:\mathrm{the}\:\mathrm{hexagon} \\ $$
Commented by naka3546 last updated on 13/Oct/19
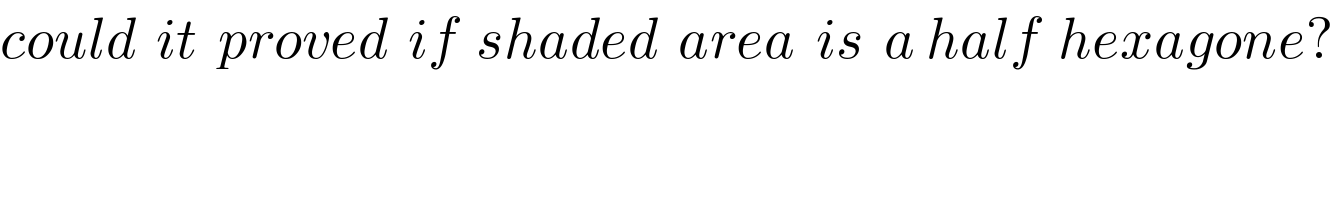
$${could}\:\:{it}\:\:{proved}\:\:{if}\:\:{shaded}\:\:{area}\:\:{is}\:\:{a}\:{half}\:\:{hexagone}? \\ $$
