Question Number 7125 by Tawakalitu. last updated on 11/Aug/16

Commented by Tawakalitu. last updated on 11/Aug/16
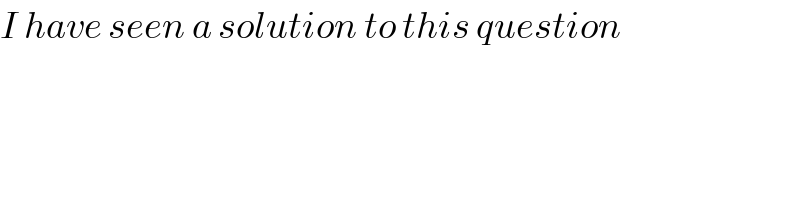
$${I}\:{have}\:{seen}\:{a}\:{solution}\:{to}\:{this}\:{question} \\ $$
Answered by sandy_suhendra last updated on 13/Aug/16
![[cos (π/7)+cos((3π)/7)+cos((5π)/7)]×((2 sin(π/7))/(2 sin (π/7))) =((2sin(π/7)cos(π/7)+2sin(π/7)cos((3π)/7)+2sin(π/7)cos((5π)/7))/(2 sin(π/7))) 2sinAcosB=sin(A+B) + sin(A−B) sin (−A) = −sinA =((sin((2π)/7)+sin 0+sin((4π)/7)−sin((2π)/7)+sin((6π)/7)−sin((4π)/7))/(2 sin (π/7))) = ((sin ((6π)/7))/(2 sin (π/7))) = ((sin [π−(π/7)])/(2 sin (π/7))) = ((sin (π/7))/(2 sin (π/7))) = (1/2)](https://www.tinkutara.com/question/Q7156.png)
$$\left[{cos}\:\frac{\pi}{\mathrm{7}}+{cos}\frac{\mathrm{3}\pi}{\mathrm{7}}+{cos}\frac{\mathrm{5}\pi}{\mathrm{7}}\right]×\frac{\mathrm{2}\:{sin}\frac{\pi}{\mathrm{7}}}{\mathrm{2}\:{sin}\:\frac{\pi}{\mathrm{7}}} \\ $$$$=\frac{\mathrm{2}{sin}\frac{\pi}{\mathrm{7}}{cos}\frac{\pi}{\mathrm{7}}+\mathrm{2}{sin}\frac{\pi}{\mathrm{7}}{cos}\frac{\mathrm{3}\pi}{\mathrm{7}}+\mathrm{2}{sin}\frac{\pi}{\mathrm{7}}{cos}\frac{\mathrm{5}\pi}{\mathrm{7}}}{\mathrm{2}\:{sin}\frac{\pi}{\mathrm{7}}} \\ $$$$\mathrm{2}{sinAcosB}={sin}\left({A}+{B}\right)\:+\:{sin}\left({A}−{B}\right) \\ $$$${sin}\:\left(−{A}\right)\:=\:−{sinA} \\ $$$$=\frac{{sin}\frac{\mathrm{2}\pi}{\mathrm{7}}+{sin}\:\mathrm{0}+{sin}\frac{\mathrm{4}\pi}{\mathrm{7}}−{sin}\frac{\mathrm{2}\pi}{\mathrm{7}}+{sin}\frac{\mathrm{6}\pi}{\mathrm{7}}−{sin}\frac{\mathrm{4}\pi}{\mathrm{7}}}{\mathrm{2}\:{sin}\:\frac{\pi}{\mathrm{7}}} \\ $$$$=\:\frac{{sin}\:\frac{\mathrm{6}\pi}{\mathrm{7}}}{\mathrm{2}\:{sin}\:\frac{\pi}{\mathrm{7}}}\:=\:\frac{{sin}\:\left[\pi−\frac{\pi}{\mathrm{7}}\right]}{\mathrm{2}\:{sin}\:\frac{\pi}{\mathrm{7}}}\:=\:\frac{{sin}\:\frac{\pi}{\mathrm{7}}}{\mathrm{2}\:{sin}\:\frac{\pi}{\mathrm{7}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Rasheed Soomro last updated on 15/Aug/16

$$\mathcal{G}^{\mathcal{OO}} \mathcal{D}\:\mathcal{A}{pproach}! \\ $$
