Question Number 71255 by ajfour last updated on 13/Oct/19
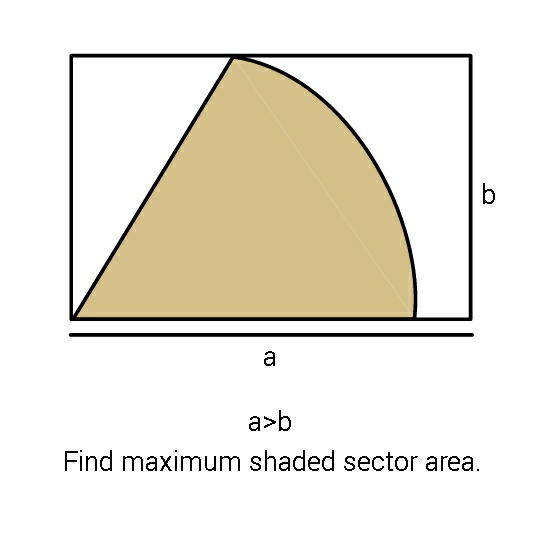
Commented by MJS last updated on 13/Oct/19
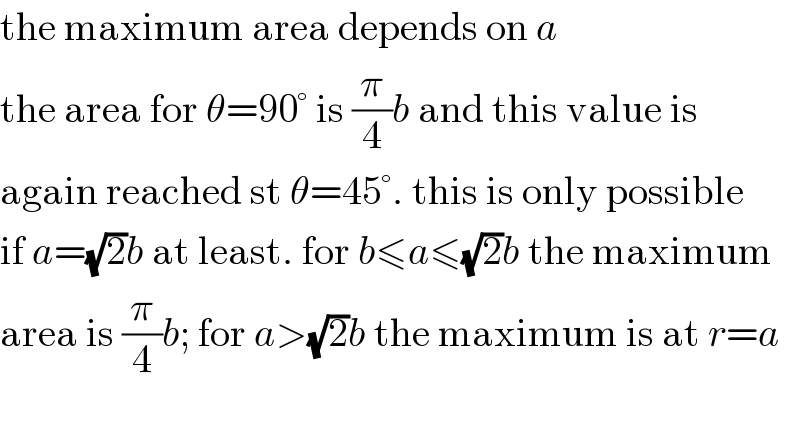
$$\mathrm{the}\:\mathrm{maximum}\:\mathrm{area}\:\mathrm{depends}\:\mathrm{on}\:{a} \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{for}\:\theta=\mathrm{90}°\:\mathrm{is}\:\frac{\pi}{\mathrm{4}}{b}\:\mathrm{and}\:\mathrm{this}\:\mathrm{value}\:\mathrm{is} \\ $$$$\mathrm{again}\:\mathrm{reached}\:\mathrm{st}\:\theta=\mathrm{45}°.\:\mathrm{this}\:\mathrm{is}\:\mathrm{only}\:\mathrm{possible} \\ $$$$\mathrm{if}\:{a}=\sqrt{\mathrm{2}}{b}\:\mathrm{at}\:\mathrm{least}.\:\mathrm{for}\:{b}\leqslant{a}\leqslant\sqrt{\mathrm{2}}{b}\:\mathrm{the}\:\mathrm{maximum} \\ $$$$\mathrm{area}\:\mathrm{is}\:\frac{\pi}{\mathrm{4}}{b};\:\mathrm{for}\:{a}>\sqrt{\mathrm{2}}{b}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{is}\:\mathrm{at}\:{r}={a} \\ $$$$ \\ $$
Commented by ajfour last updated on 13/Oct/19
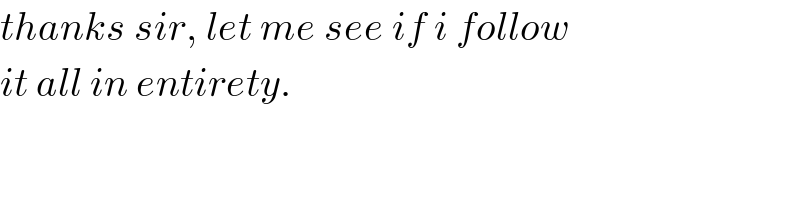
$${thanks}\:{sir},\:{let}\:{me}\:{see}\:{if}\:{i}\:{follow} \\ $$$${it}\:{all}\:{in}\:{entirety}. \\ $$
Answered by ajfour last updated on 13/Oct/19
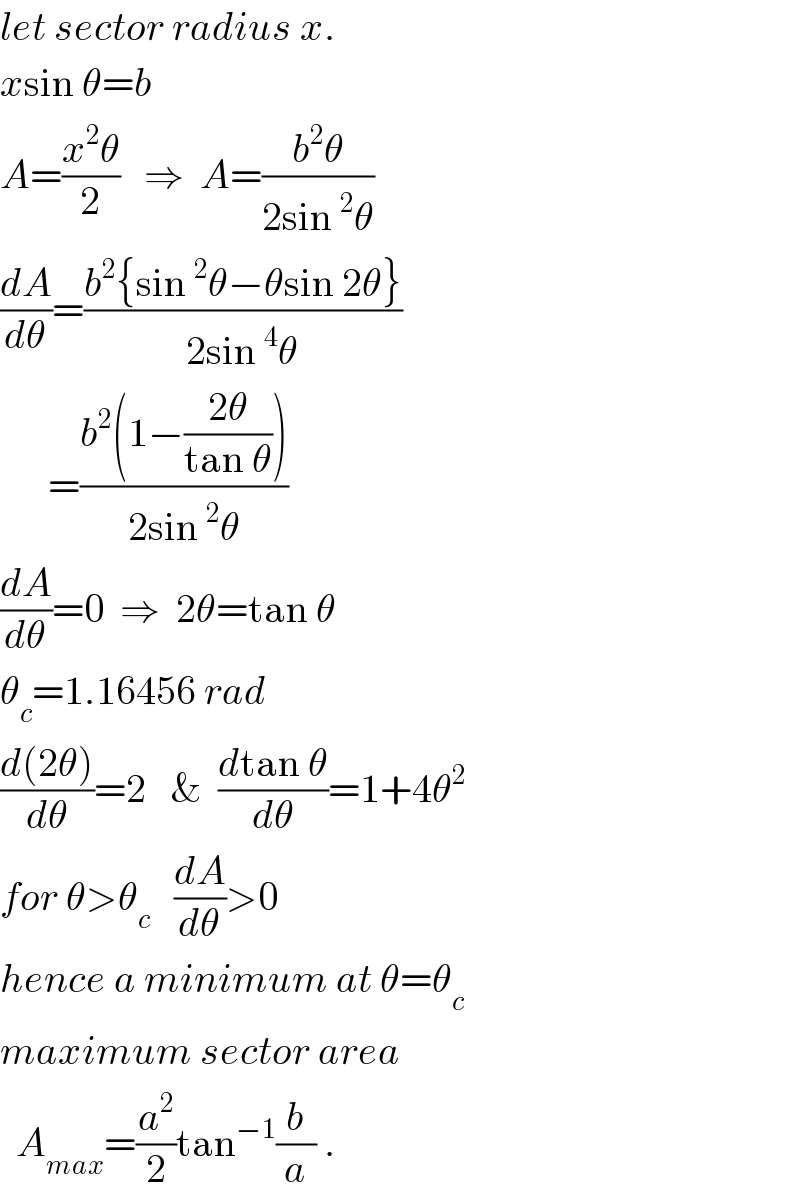
$${let}\:{sector}\:{radius}\:{x}. \\ $$$${x}\mathrm{sin}\:\theta={b}\: \\ $$$${A}=\frac{{x}^{\mathrm{2}} \theta}{\mathrm{2}}\:\:\:\Rightarrow\:\:{A}=\frac{{b}^{\mathrm{2}} \theta}{\mathrm{2sin}\:^{\mathrm{2}} \theta} \\ $$$$\frac{{dA}}{{d}\theta}=\frac{{b}^{\mathrm{2}} \left\{\mathrm{sin}\:^{\mathrm{2}} \theta−\theta\mathrm{sin}\:\mathrm{2}\theta\right\}}{\mathrm{2sin}\:^{\mathrm{4}} \theta} \\ $$$$\:\:\:\:\:\:=\frac{{b}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{2}\theta}{\mathrm{tan}\:\theta}\right)}{\mathrm{2sin}\:^{\mathrm{2}} \theta} \\ $$$$\frac{{dA}}{{d}\theta}=\mathrm{0}\:\:\Rightarrow\:\:\mathrm{2}\theta=\mathrm{tan}\:\theta \\ $$$$\theta_{{c}} =\mathrm{1}.\mathrm{16456}\:{rad} \\ $$$$\frac{{d}\left(\mathrm{2}\theta\right)}{{d}\theta}=\mathrm{2}\:\:\:\&\:\:\frac{{d}\mathrm{tan}\:\theta}{{d}\theta}=\mathrm{1}+\mathrm{4}\theta^{\mathrm{2}} \\ $$$${for}\:\theta>\theta_{{c}} \:\:\:\frac{{dA}}{{d}\theta}>\mathrm{0} \\ $$$${hence}\:{a}\:{minimum}\:{at}\:\theta=\theta_{{c}} \\ $$$${maximum}\:{sector}\:{area} \\ $$$$\:\:{A}_{{max}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \frac{{b}}{{a}}\:. \\ $$
Commented by ajfour last updated on 13/Oct/19
$${someone}\:{answer}\:{it}\:{please}. \\ $$
