Question Number 7126 by Tawakalitu. last updated on 11/Aug/16
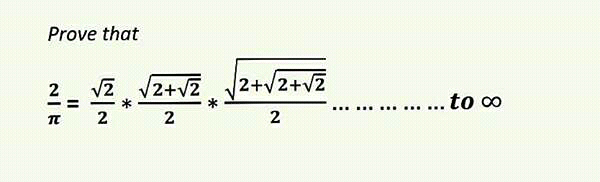
Commented by Tawakalitu. last updated on 11/Aug/16
$${I}\:{need}\:{solution}\:{to}\:{this}\:{one}.\:{thanks}\:{in}\:{advance} \\ $$
Commented by Yozzii last updated on 13/Aug/16

$${u}_{{n}+\mathrm{1}} =\sqrt{\mathrm{2}+{u}_{{n}} } \\ $$$${u}_{\mathrm{0}} =\mathrm{0}\Rightarrow{u}_{\mathrm{1}} =\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{u}_{\mathrm{2}} =\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow{u}_{\mathrm{3}} =\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}} \\ $$$${u}_{{n}+\mathrm{1}} ^{\mathrm{2}} −{u}_{{n}} −\mathrm{2}=\mathrm{0} \\ $$$$−−−−−−−−−−−−−−−−−−− \\ $$$$\left({Under}\:{construction}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 13/Aug/16
$${Thank}\:{you}\:{for}\:{your}\:{time}\:{sir}. \\ $$
