Question Number 71327 by TawaTawa last updated on 13/Oct/19
Answered by mind is power last updated on 13/Oct/19

$$\mathrm{ferma}\:\mathrm{lemma}\: \\ $$$$\mathrm{x}^{\mathrm{5}} =\mathrm{x}\left(\mathrm{5}\right) \\ $$$$\mathrm{x}^{\mathrm{4}} =\mathrm{1}\left(\mathrm{5}\right)\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if}\:\mathrm{x}\neq\mathrm{0} \\ $$$$\:\mathrm{x}=\mathrm{0}\:\mathrm{solution} \\ $$$$\mathrm{x}\neq\mathrm{0a}\Leftrightarrow\mathrm{2x}+\mathrm{2x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2x}^{\mathrm{2}} −\mathrm{x}=\mathrm{0}\left(\mathrm{5}\right) \\ $$$$\Rightarrow\mathrm{0}=\mathrm{0}\left(\mathrm{5}\right) \\ $$$$\Rightarrow\mathrm{always}\:\mathrm{true} \\ $$$$\left.\mathrm{b}\right)\:\mathrm{x}\:\mathrm{solution}\:\Rightarrow\mathrm{x}^{\mathrm{4}} +\mathrm{x}\neq\mathrm{0}\left(\mathrm{7}\right) \\ $$$$\mathrm{all}\:\mathrm{think}\:\mathrm{below}\:\mathrm{is}\:\mathrm{modd}\left(\mathrm{7}\right) \\ $$$$\mathrm{x}^{\mathrm{4}} +\mathrm{x}=\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)=\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{6}\right) \\ $$$$=\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{3}\right)\left(\mathrm{x}+\mathrm{2}\right)=\mathrm{x}\left(\mathrm{x}−\mathrm{6}\right)\left(\mathrm{x}−\mathrm{3}\right)\left(\mathrm{x}−\mathrm{5}\right) \\ $$$$\mathrm{x}^{\mathrm{4}} +\mathrm{x}=\mathrm{0}\left(\mathrm{7}\right)\:\mathrm{if}\:\mathrm{x}=\mathrm{0},\mathrm{3},\mathrm{5},\mathrm{6}\left(\mathrm{7}\right) \\ $$$$\mathrm{just}\:\mathrm{to}\:\mathrm{test}\:\mathrm{1},\mathrm{2},\mathrm{4} \\ $$$$\mathrm{fir}\:\mathrm{2}\:\mid\mathrm{x}^{\mathrm{4}} +\mathrm{x}=\mathrm{18}=\mathrm{4}\left(\mathrm{7}\right)\:\mathrm{not}\:\mathrm{solution}\: \\ $$$$\mathrm{x}=\mathrm{4}\mid\mathrm{x}^{\mathrm{4}} +\mathrm{x}+\mathrm{2}=\mathrm{2}^{\mathrm{8}} +\mathrm{4}+\mathrm{2}=\mathrm{1}\left(\mathrm{7}\right) \\ $$$$\mathrm{x}=\mathrm{1}\Rightarrow\mathrm{x}^{\mathrm{4}} +\mathrm{x}+\mathrm{2}=\mathrm{4}\left(\mathrm{7}\right)\:\mathrm{not}\:\mathrm{slution} \\ $$$$\mathrm{S}=\varnothing \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by TawaTawa last updated on 14/Oct/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mind is power last updated on 14/Oct/19

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$
Answered by delloptiplex last updated on 14/Oct/19
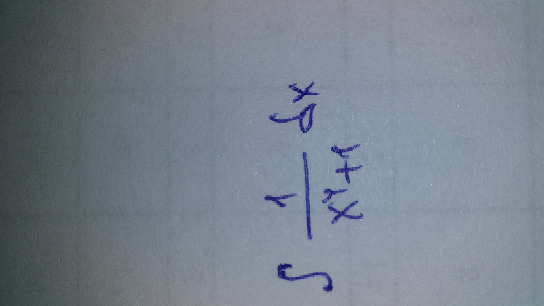
Commented by mathmax by abdo last updated on 14/Oct/19
$${this}\:{integral}\:{was}\:{solved}\:\:{see}\:{the}\:{platform}. \\ $$
