Question Number 71371 by rajesh4661kumar@gmail.com last updated on 14/Oct/19

Commented by prakash jain last updated on 15/Oct/19
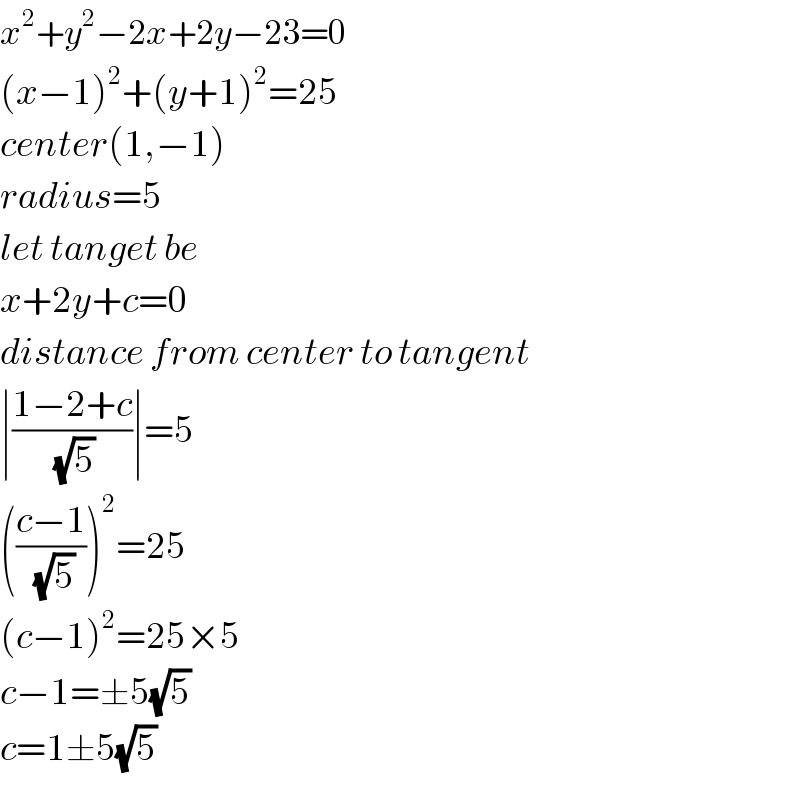
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}{y}−\mathrm{23}=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\left({y}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{25} \\ $$$${center}\left(\mathrm{1},−\mathrm{1}\right) \\ $$$${radius}=\mathrm{5} \\ $$$${let}\:{tanget}\:{be} \\ $$$${x}+\mathrm{2}{y}+{c}=\mathrm{0} \\ $$$${distance}\:{from}\:{center}\:{to}\:{tangent} \\ $$$$\mid\frac{\mathrm{1}−\mathrm{2}+{c}}{\:\sqrt{\mathrm{5}}}\mid=\mathrm{5} \\ $$$$\left(\frac{{c}−\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} =\mathrm{25} \\ $$$$\left({c}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{25}×\mathrm{5} \\ $$$${c}−\mathrm{1}=\pm\mathrm{5}\sqrt{\mathrm{5}} \\ $$$${c}=\mathrm{1}\pm\mathrm{5}\sqrt{\mathrm{5}} \\ $$
