Question Number 7138 by Tawakalitu. last updated on 12/Aug/16
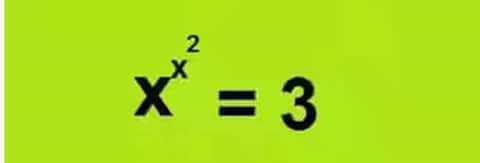
Answered by Yozzii last updated on 13/Aug/16
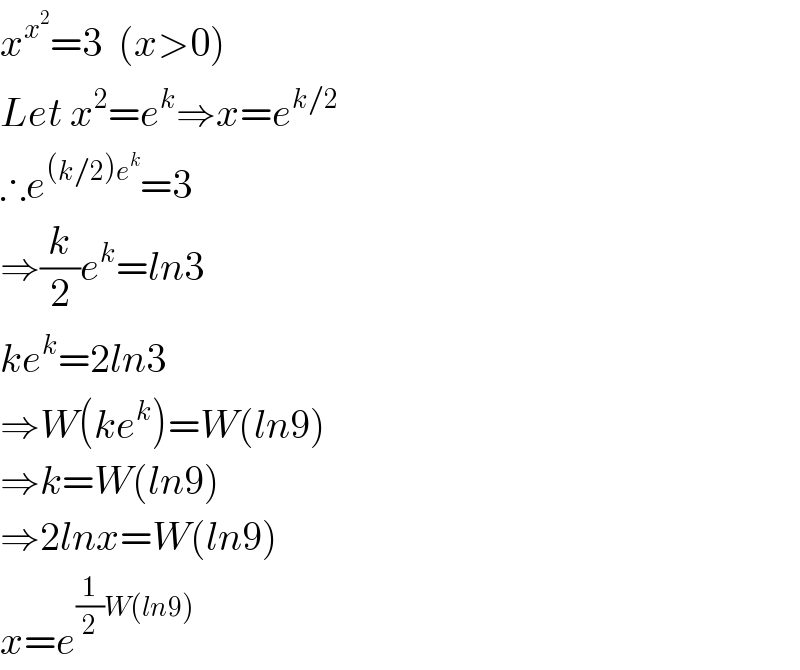
$${x}^{{x}^{\mathrm{2}} } =\mathrm{3}\:\:\left({x}>\mathrm{0}\right) \\ $$$${Let}\:{x}^{\mathrm{2}} ={e}^{{k}} \Rightarrow{x}={e}^{{k}/\mathrm{2}} \\ $$$$\therefore{e}^{\left({k}/\mathrm{2}\right){e}^{{k}} } =\mathrm{3} \\ $$$$\Rightarrow\frac{{k}}{\mathrm{2}}{e}^{{k}} ={ln}\mathrm{3} \\ $$$${ke}^{{k}} =\mathrm{2}{ln}\mathrm{3} \\ $$$$\Rightarrow{W}\left({ke}^{{k}} \right)={W}\left({ln}\mathrm{9}\right) \\ $$$$\Rightarrow{k}={W}\left({ln}\mathrm{9}\right) \\ $$$$\Rightarrow\mathrm{2}{lnx}={W}\left({ln}\mathrm{9}\right) \\ $$$${x}={e}^{\frac{\mathrm{1}}{\mathrm{2}}{W}\left({ln}\mathrm{9}\right)} \\ $$
