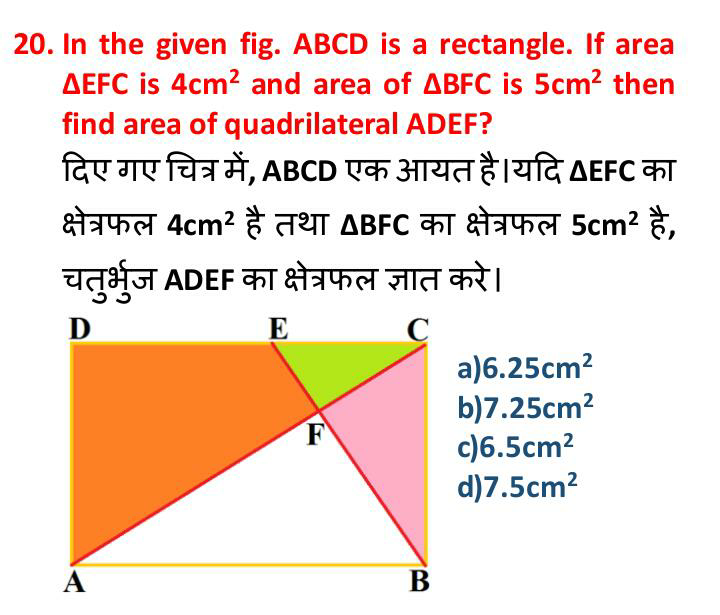
Question Number 71410 by TawaTawa last updated on 15/Oct/19
Answered by MJS last updated on 15/Oct/19

$${A}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{{p}}\\{\mathrm{0}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{{p}}\\{{q}}\end{pmatrix}\:\:{D}=\begin{pmatrix}{\mathrm{0}}\\{{q}}\end{pmatrix} \\ $$$${DC}:\:{y}={q} \\ $$$${AC}:\:{y}=\frac{{q}}{{p}}{x} \\ $$$${BE}:\:{y}=−\frac{{p}}{{q}}{x}+\frac{{p}^{\mathrm{2}} }{{q}} \\ $$$${E}={BE}\cap{DC}=\begin{pmatrix}{\frac{{p}^{\mathrm{2}} −{q}^{\mathrm{2}} }{{p}}}\\{{q}}\end{pmatrix} \\ $$$${F}={AC}\cap{BE}=\begin{pmatrix}{\frac{{p}^{\mathrm{3}} }{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}\\{\frac{{p}^{\mathrm{2}} {q}}{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}\end{pmatrix} \\ $$$$\mathrm{area}\:\left({ABF}\right)\:=\frac{{p}^{\mathrm{3}} {q}}{\mathrm{2}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)} \\ $$$$\mathrm{area}\:\left({BCF}\right)\:=\frac{{pq}^{\mathrm{3}} }{\mathrm{2}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)} \\ $$$$\mathrm{area}\:\left({CEF}\right)\:=\frac{{q}^{\mathrm{5}} }{\mathrm{2}{p}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)} \\ $$$$\mathrm{area}\:\left({ADEF}\right)\:=\frac{{q}\left({p}^{\mathrm{4}} +{p}^{\mathrm{2}} {q}^{\mathrm{2}} −{q}^{\mathrm{4}} \right)}{\mathrm{2}{p}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)} \\ $$$$ \\ $$$$\frac{{pq}^{\mathrm{3}} }{\mathrm{2}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)}=\mathrm{5}\:\Rightarrow\:{p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\frac{{pq}^{\mathrm{3}} }{\mathrm{10}} \\ $$$$\frac{{q}^{\mathrm{5}} }{\mathrm{2}{p}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)}=\mathrm{4}\:\Rightarrow\:{p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\frac{{q}^{\mathrm{5}} }{\mathrm{8}{p}} \\ $$$$\frac{{pq}^{\mathrm{3}} }{\mathrm{10}}=\frac{{q}^{\mathrm{5}} }{\mathrm{8}{p}}\:\Rightarrow{q}=\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{5}}{p}\:\Rightarrow\:{p}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt[{\mathrm{4}}]{\mathrm{125}}\wedge{q}=\mathrm{3}\sqrt[{\mathrm{4}}]{\mathrm{5}} \\ $$$$\Rightarrow\:\mathrm{area}\:\left({ABF}\right)\:=\frac{{p}^{\mathrm{3}} {q}}{\mathrm{2}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)}=\frac{\mathrm{25}}{\mathrm{4}}=\mathrm{6}.\mathrm{25} \\ $$$$\mathrm{area}\:\left({ADEF}\right)\:=\frac{{q}\left({p}^{\mathrm{4}} +{p}^{\mathrm{2}} {q}^{\mathrm{2}} −{q}^{\mathrm{4}} \right)}{\mathrm{2}{p}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)}=\frac{\mathrm{29}}{\mathrm{4}}=\mathrm{7}.\mathrm{25} \\ $$
Commented by TawaTawa last updated on 15/Oct/19
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$
Commented by TawaTawa last updated on 15/Oct/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
