Question Number 71490 by oyemi kemewari last updated on 16/Oct/19

Commented by mathmax by abdo last updated on 16/Oct/19
![let A=∫_0 ^(1/2) ((1+(√3))/((^4 (√((1+x)^2 (1−x)^6 ))))dx ⇒A=(1+(√3))∫_0 ^(1/2) (dx/( (√(1+x))(1−x)^(2/3) )) changement x=cos(2t) give t=(1/2)arcosx A=(1+(√3))∫_(π/4) ^(π/6) ((−2sin2t dt)/( (√(2cos^2 t))(2sin^2 t)^(3/2) )) =((2(1+(√3)))/2^((1/2)+(3/2)) ) ∫_(π/6) ^(π/4) ((sin(2t))/(cost(sint)(sint)^2 ))dt =((2(1+(√3)))/2^2 ) ∫_(π/6) ^(π/4) ((2sint cost)/(cost sint (sint)^2 ))dt=(1+(√3))∫_(π/6) ^(π/4) (dt/(sin^2 t)) =(1+(√3))∫_(π/6) ^(π/4) (dt/((1−cos(2t))/2)) =2(1+(√3)) ∫_(π/6) ^(π/4) (dt/(1−cos(2t))) but ∫_(π/6) ^(π/4) (dt/(1−cos(2t))) =_(tant=u) ∫_(1/( (√3))) ^1 (1/(1−((1−u^2 )/(1+u^2 )))) (du/(1+u^2 )) =∫_(1/( (√3))) ^1 (du/(1+u^2 −1+u^2 )) =∫_(1/( (√3))) ^1 (du/(2u^2 )) =(1/2)[−(1/u)]_(1/( (√3))) ^1 =(1/2)((√3)−1) ⇒A=2(1+(√3))×(((√3)−1)/2) =((√3))^2 −1 =2 ⇒ A =2](https://www.tinkutara.com/question/Q71503.png)
$${let}\:{A}=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\left(^{\mathrm{4}} \sqrt{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{6}} }\right.}{dx}\:\Rightarrow{A}=\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:\frac{{dx}}{\:\sqrt{\mathrm{1}+{x}}\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} } \\ $$$${changement}\:{x}={cos}\left(\mathrm{2}{t}\right)\:{give}\:{t}=\frac{\mathrm{1}}{\mathrm{2}}{arcosx} \\ $$$${A}=\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{6}}} \:\:\:\frac{−\mathrm{2}{sin}\mathrm{2}{t}\:{dt}}{\:\sqrt{\mathrm{2}{cos}^{\mathrm{2}} {t}}\left(\mathrm{2}{sin}^{\mathrm{2}} {t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=\frac{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)}{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}} }\:\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{sin}\left(\mathrm{2}{t}\right)}{{cost}\left({sint}\right)\left({sint}\right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)}{\mathrm{2}^{\mathrm{2}} }\:\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{2}{sint}\:{cost}}{{cost}\:{sint}\:\left({sint}\right)^{\mathrm{2}} }{dt}=\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dt}}{{sin}^{\mathrm{2}} {t}} \\ $$$$=\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{dt}}{\frac{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}}\:=\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\:\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{dt}}{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)} \\ $$$${but}\:\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dt}}{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)}\:=_{{tant}={u}} \:\:\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} −\mathrm{1}+{u}^{\mathrm{2}} }\:=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \:\:\frac{{du}}{\mathrm{2}{u}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\left[−\frac{\mathrm{1}}{{u}}\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\:\Rightarrow{A}=\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)×\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}\:=\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{1}\:=\mathrm{2}\:\Rightarrow \\ $$$${A}\:=\mathrm{2} \\ $$
Commented by mathmax by abdo last updated on 16/Oct/19

$${error}\:{of}\:{typo}\:{at}\:{first}\:{line}\:{A}=\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:\frac{{dx}}{\:\sqrt{\mathrm{1}+{x}}\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$
Answered by mind is power last updated on 16/Oct/19
![x=sin(α) ∫_0 ^(π/6) ((1+(√3))/( (((1+sin(α))^2 (1−sin(α))^6 ))^(1/4) ))cos(α)dα 1+_− sin(α)=(cos((α/2))+_− sin((α/2)))^2 ∫_0 ^(π/6) ((1+(√3))/( (((1+sin(α))^2 (1−sin(α))^6 ))^(1/4) ))cos(α)dα=∫_0 ^(π/6) (((1+(√3))cos(α)dα)/( (((cos((α/2))+sin((α/2)))^4 (cos((α/2))−sin((α/2)))^(12) ))^(1/4) )) =∫_0 ^(π/6) (((1+(√3))cos(α))/((cos((α/2))+sin((α/2))).(cos((α/2))−sin((α/2)))^3 )) =∫_0 ^(π/6) (((1+(√3))cos(α)dα)/(cos(α).(cos((α/2))−sin((α/2)))^2 )) =∫_0 ^(π/6) ((1+(√3))/(cos^2 ((α/2))(1−tg((α/2)))^2 ))dα =(1+(√3))∫_0 ^(π/6) ((1+tg^2 ((α/2)))/((1−tg((α/2)))^2 ))dα =2(1+(√3)).[(1/(1−tg((α/2))))]_0 ^(π/6) =2(1+(√3)).(1/(1−tg((π/(12)))))−2−2(√3)=((2(1+(√3))(((1+cos((π/6))+sin((π/6)))/2)))/(cos((π/6))))−2−2(√3) =(((1+(√3))(1+((√3)/2)+(1/2)))/((√3)/2))=(((3+(√3))(1+(√3)))/( (√3))) −2−2(√3)=4+2(√3)−2−2(√3)=2](https://www.tinkutara.com/question/Q71494.png)
$$\mathrm{x}=\mathrm{sin}\left(\alpha\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\:\sqrt[{\mathrm{4}}]{\left(\mathrm{1}+\mathrm{sin}\left(\alpha\right)\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\left(\alpha\right)\right)^{\mathrm{6}} }}\mathrm{cos}\left(\alpha\right)\mathrm{d}\alpha \\ $$$$\mathrm{1}\underset{−} {+}\mathrm{sin}\left(\alpha\right)=\left(\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}}\right)\underset{−} {+}\mathrm{sin}\left(\frac{\alpha}{\mathrm{2}}\right)\right)^{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\:\sqrt[{\mathrm{4}}]{\left(\mathrm{1}+\mathrm{sin}\left(\alpha\right)\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\left(\alpha\right)\right)^{\mathrm{6}} }}\mathrm{cos}\left(\alpha\right)\mathrm{d}\alpha=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \frac{\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\mathrm{cos}\left(\alpha\right)\mathrm{d}\alpha}{\:\sqrt[{\mathrm{4}}]{\left(\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}}\right)+\mathrm{sin}\left(\frac{\alpha}{\mathrm{2}}\right)\right)^{\mathrm{4}} \left(\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}}\right)−\mathrm{sin}\left(\frac{\alpha}{\mathrm{2}}\right)\right)^{\mathrm{12}} }} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \frac{\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\mathrm{cos}\left(\alpha\right)}{\left(\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}}\right)+\mathrm{sin}\left(\frac{\alpha}{\mathrm{2}}\right)\right).\left(\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}}\right)−\mathrm{sin}\left(\frac{\alpha}{\mathrm{2}}\right)\right)^{\mathrm{3}} } \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \frac{\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\mathrm{cos}\left(\alpha\right)\mathrm{d}\alpha}{\mathrm{cos}\left(\alpha\right).\left(\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}}\right)−\mathrm{sin}\left(\frac{\alpha}{\mathrm{2}}\right)\right)^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{cos}^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}\right)\left(\mathrm{1}−\mathrm{tg}\left(\frac{\alpha}{\mathrm{2}}\right)\right)^{\mathrm{2}} }\mathrm{d}\alpha \\ $$$$=\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \frac{\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}\right)}{\left(\mathrm{1}−\mathrm{tg}\left(\frac{\alpha}{\mathrm{2}}\right)\right)^{\mathrm{2}} }\mathrm{d}\alpha \\ $$$$=\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right).\left[\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tg}\left(\frac{\alpha}{\mathrm{2}}\right)}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} =\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right).\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tg}\left(\frac{\pi}{\mathrm{12}}\right)}−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{3}}=\frac{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\left(\frac{\mathrm{1}+\mathrm{cos}\left(\frac{\pi}{\mathrm{6}}\right)+\mathrm{sin}\left(\frac{\pi}{\mathrm{6}}\right)}{\mathrm{2}}\right)}{\mathrm{cos}\left(\frac{\pi}{\mathrm{6}}\right)}−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$=\frac{\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\left(\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}=\frac{\left(\mathrm{3}+\sqrt{\mathrm{3}}\right)\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)}{\:\sqrt{\mathrm{3}}}\:−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{3}}=\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{3}}=\mathrm{2} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by MJS last updated on 16/Oct/19

$$\mathrm{I}\:\mathrm{guess}\:\mathrm{something}\:\mathrm{went}\:\mathrm{wrong}… \\ $$
Commented by mind is power last updated on 16/Oct/19
![yeah [f(x)]_0 ^(π/2) =f((π/2))−f(0) i firget too substract f(0)](https://www.tinkutara.com/question/Q71498.png)
$$\mathrm{yeah}\:\:\:\left[\mathrm{f}\left(\mathrm{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{f}\left(\frac{\pi}{\mathrm{2}}\right)−\mathrm{f}\left(\mathrm{0}\right)\:\:\mathrm{i}\:\mathrm{firget}\:\mathrm{too}\:\mathrm{substract}\:\mathrm{f}\left(\mathrm{0}\right)\: \\ $$
Commented by mathmax by abdo last updated on 16/Oct/19
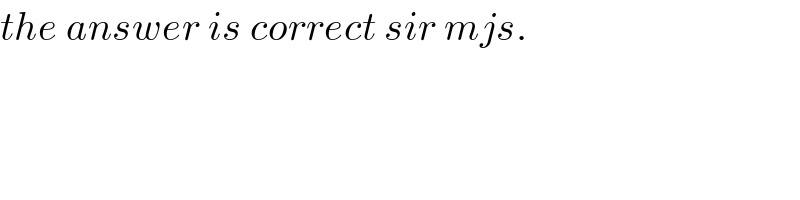
$${the}\:{answer}\:{is}\:{correct}\:{sir}\:{mjs}. \\ $$
Answered by MJS last updated on 16/Oct/19
![∫((1+(√3))/( (((1+x)^2 (1−x)^6 ))^(1/4) ))dx= =(1+(√3))∫(dx/( (√(∣x−1∣^3 ∣x+1∣)))) 0≤x≤(1/2) ⇒ (1/( (√(∣x−1∣^3 ∣x+1∣))))=(1/( (√((−x+1)^3 (x+1))))) ∫(dx/( (√((−x+1)^3 (x+1)))))= [t=arcsin (√((−x+1)/2)) → dx=−2(√((−x+1)(x+1)))] =−∫(dt/(sin^2 t))=(1/(tan t))=((√(x+1))/( (√(−x+1))))+C ∫_0 ^(1/2) ((1+(√3))/( (((1+x)^2 (1−x)^6 ))^(1/4) ))dx=2](https://www.tinkutara.com/question/Q71495.png)
$$\int\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\:\sqrt[{\mathrm{4}}]{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{6}} }}{dx}= \\ $$$$=\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\int\frac{{dx}}{\:\sqrt{\mid{x}−\mathrm{1}\mid^{\mathrm{3}} \mid{x}+\mathrm{1}\mid}} \\ $$$$\mathrm{0}\leqslant{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:\frac{\mathrm{1}}{\:\sqrt{\mid{x}−\mathrm{1}\mid^{\mathrm{3}} \mid{x}+\mathrm{1}\mid}}=\frac{\mathrm{1}}{\:\sqrt{\left(−{x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{1}\right)}} \\ $$$$\int\frac{{dx}}{\:\sqrt{\left(−{x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{1}\right)}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{arcsin}\:\sqrt{\frac{−{x}+\mathrm{1}}{\mathrm{2}}}\:\rightarrow\:{dx}=−\mathrm{2}\sqrt{\left(−{x}+\mathrm{1}\right)\left({x}+\mathrm{1}\right)}\right] \\ $$$$=−\int\frac{{dt}}{\mathrm{sin}^{\mathrm{2}} \:{t}}=\frac{\mathrm{1}}{\mathrm{tan}\:{t}}=\frac{\sqrt{{x}+\mathrm{1}}}{\:\sqrt{−{x}+\mathrm{1}}}+{C} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}/\mathrm{2}} {\int}}\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\:\sqrt[{\mathrm{4}}]{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{6}} }}{dx}=\mathrm{2} \\ $$
