Question Number 71513 by aliesam last updated on 16/Oct/19
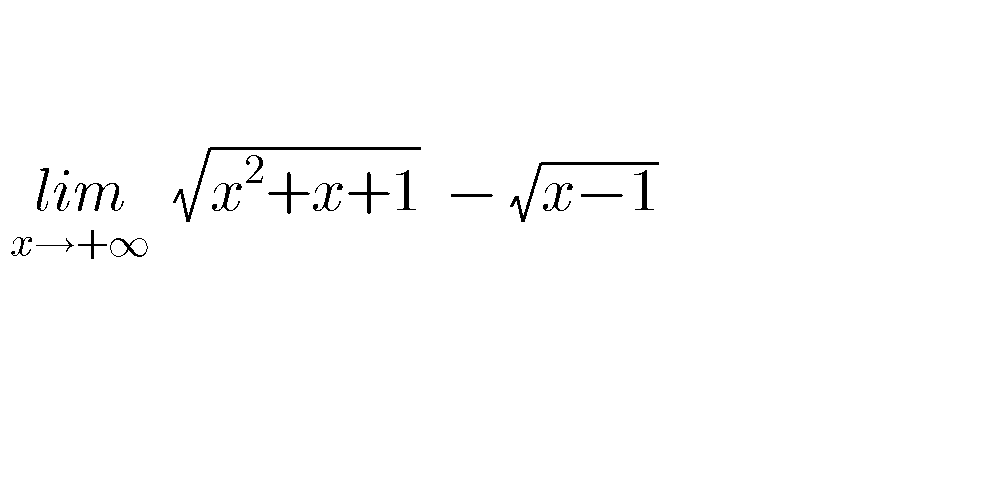
Commented by kaivan.ahmadi last updated on 16/Oct/19
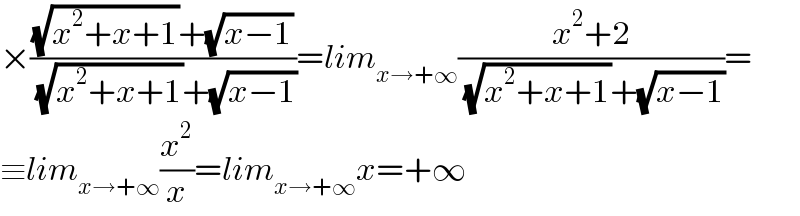
$$×\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\sqrt{{x}−\mathrm{1}}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\sqrt{{x}−\mathrm{1}}}={lim}_{{x}\rightarrow+\infty} \frac{{x}^{\mathrm{2}} +\mathrm{2}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\sqrt{{x}−\mathrm{1}}}= \\ $$$$\equiv{lim}_{{x}\rightarrow+\infty} \frac{{x}^{\mathrm{2}} }{{x}}={lim}_{{x}\rightarrow+\infty} {x}=+\infty \\ $$
Commented by mathmax by abdo last updated on 16/Oct/19
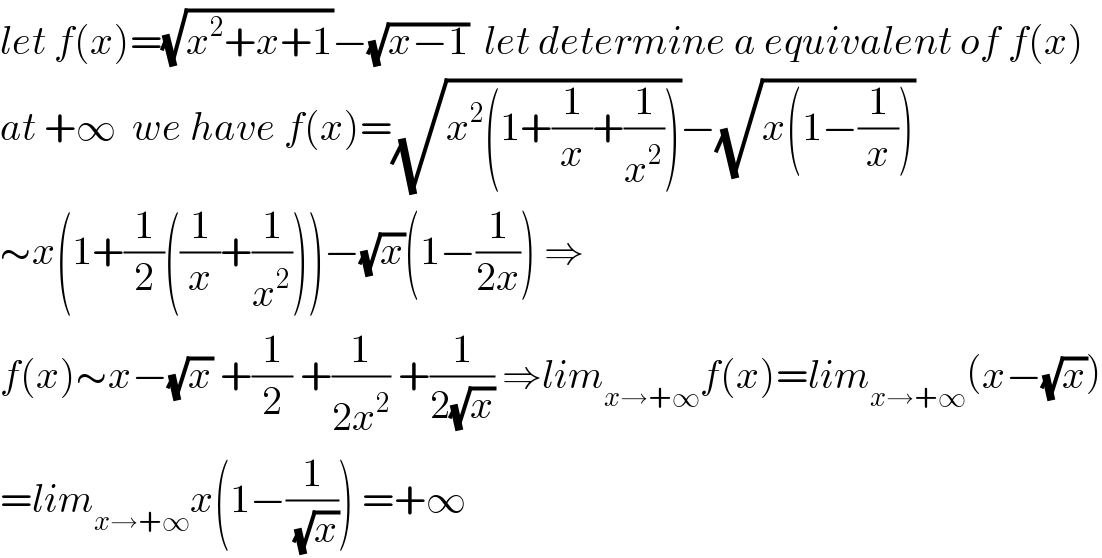
$${let}\:{f}\left({x}\right)=\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{1}}\:\:{let}\:{determine}\:{a}\:{equivalent}\:{of}\:{f}\left({x}\right) \\ $$$${at}\:+\infty\:\:{we}\:{have}\:{f}\left({x}\right)=\sqrt{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}−\sqrt{{x}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)} \\ $$$$\sim{x}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\right)−\sqrt{{x}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{x}}\right)\:\Rightarrow \\ $$$${f}\left({x}\right)\sim{x}−\sqrt{{x}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\:\Rightarrow{lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)={lim}_{{x}\rightarrow+\infty} \left({x}−\sqrt{{x}}\right) \\ $$$$={lim}_{{x}\rightarrow+\infty} {x}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{{x}}}\right)\:=+\infty \\ $$
