Question Number 71550 by mhmd last updated on 17/Oct/19
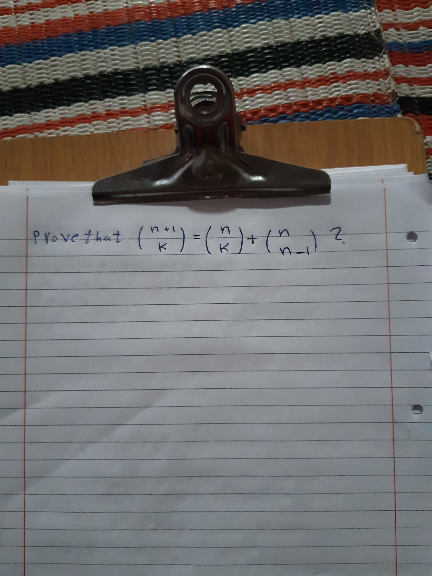
Answered by MJS last updated on 17/Oct/19
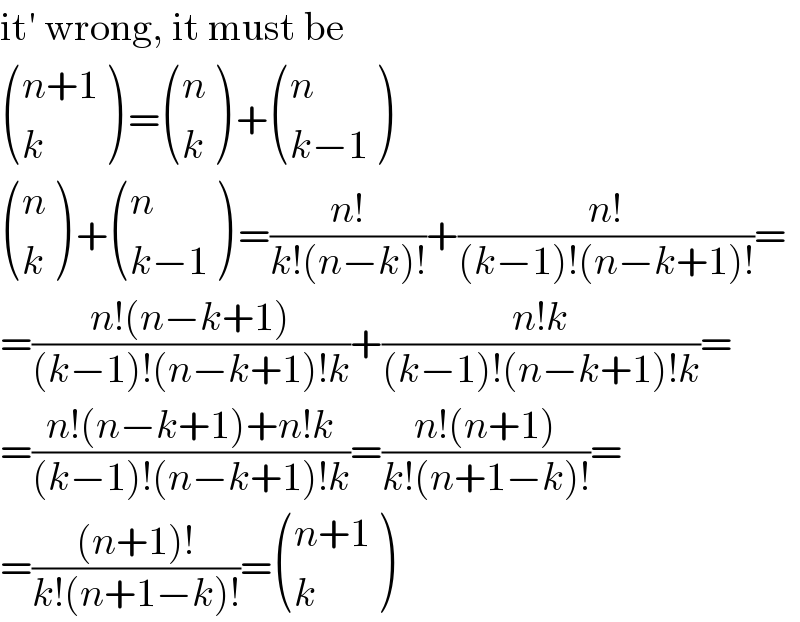
$$\mathrm{it}'\:\mathrm{wrong},\:\mathrm{it}\:\mathrm{must}\:\mathrm{be} \\ $$$$\begin{pmatrix}{{n}+\mathrm{1}}\\{{k}}\end{pmatrix}\:=\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:+\begin{pmatrix}{{n}}\\{{k}−\mathrm{1}}\end{pmatrix} \\ $$$$\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:+\begin{pmatrix}{{n}}\\{{k}−\mathrm{1}}\end{pmatrix}\:=\frac{{n}!}{{k}!\left({n}−{k}\right)!}+\frac{{n}!}{\left({k}−\mathrm{1}\right)!\left({n}−{k}+\mathrm{1}\right)!}= \\ $$$$=\frac{{n}!\left({n}−{k}+\mathrm{1}\right)}{\left({k}−\mathrm{1}\right)!\left({n}−{k}+\mathrm{1}\right)!{k}}+\frac{{n}!{k}}{\left({k}−\mathrm{1}\right)!\left({n}−{k}+\mathrm{1}\right)!{k}}= \\ $$$$=\frac{{n}!\left({n}−{k}+\mathrm{1}\right)+{n}!{k}}{\left({k}−\mathrm{1}\right)!\left({n}−{k}+\mathrm{1}\right)!{k}}=\frac{{n}!\left({n}+\mathrm{1}\right)}{{k}!\left({n}+\mathrm{1}−{k}\right)!}= \\ $$$$=\frac{\left({n}+\mathrm{1}\right)!}{{k}!\left({n}+\mathrm{1}−{k}\right)!}=\begin{pmatrix}{{n}+\mathrm{1}}\\{{k}}\end{pmatrix} \\ $$
