Question Number 7163 by Tawakalitu. last updated on 14/Aug/16
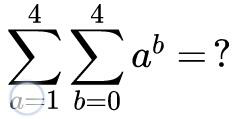
Commented by sou1618 last updated on 14/Aug/16
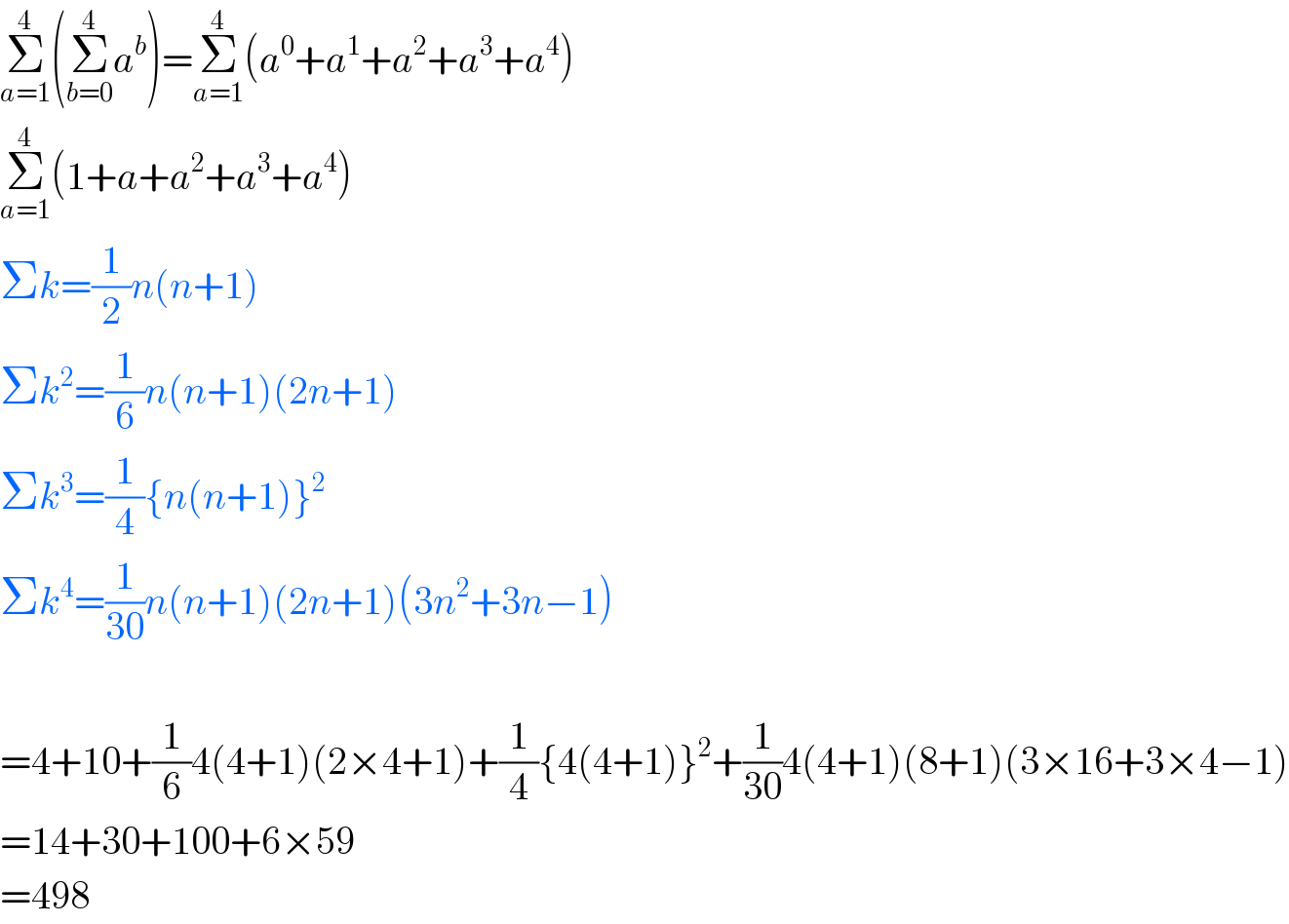
$$\underset{{a}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}\left(\underset{{b}=\mathrm{0}} {\overset{\mathrm{4}} {\sum}}{a}^{{b}} \right)=\underset{{a}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}\left({a}^{\mathrm{0}} +{a}^{\mathrm{1}} +{a}^{\mathrm{2}} +{a}^{\mathrm{3}} +{a}^{\mathrm{4}} \right) \\ $$$$\underset{{a}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}\left(\mathrm{1}+{a}+{a}^{\mathrm{2}} +{a}^{\mathrm{3}} +{a}^{\mathrm{4}} \right) \\ $$$$\Sigma{k}=\frac{\mathrm{1}}{\mathrm{2}}{n}\left({n}+\mathrm{1}\right) \\ $$$$\Sigma{k}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{6}}{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$$$\Sigma{k}^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{4}}\left\{{n}\left({n}+\mathrm{1}\right)\right\}^{\mathrm{2}} \\ $$$$\Sigma{k}^{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{30}}{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{1}\right) \\ $$$$ \\ $$$$=\mathrm{4}+\mathrm{10}+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{4}\left(\mathrm{4}+\mathrm{1}\right)\left(\mathrm{2}×\mathrm{4}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left\{\mathrm{4}\left(\mathrm{4}+\mathrm{1}\right)\right\}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{30}}\mathrm{4}\left(\mathrm{4}+\mathrm{1}\right)\left(\mathrm{8}+\mathrm{1}\right)\left(\mathrm{3}×\mathrm{16}+\mathrm{3}×\mathrm{4}−\mathrm{1}\right) \\ $$$$=\mathrm{14}+\mathrm{30}+\mathrm{100}+\mathrm{6}×\mathrm{59} \\ $$$$=\mathrm{498} \\ $$
Commented by Tawakalitu. last updated on 14/Aug/16
$${Wow},\:{I}\:{really}\:{appreciate}\:{your}\:{effort}.{Thanks}\:{so}\:{much}. \\ $$
