Question-71717

Question Number 71717 by peter frank last updated on 19/Oct/19

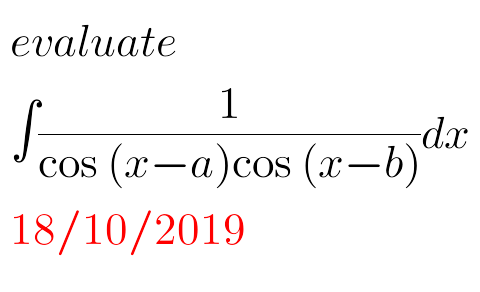
Commented by mathmax by abdo last updated on 19/Oct/19

let I=∫ (dx/(cos(x−a)cos(x−b))) ⇒I=∫ ((2dx)/(cos(2x−a−b)+cos(a−b))) =_(2x−(a+b)=t) ∫ (dt/(cost +λ)) with λ=cos(a−b) changement tan((t/2))=u give ∫ (dt/(cost +λ)) =∫ (1/(((1−u^2 )/(1+u^2 ))+λ))((2du)/(1+u^2 )) =∫ ((2du)/(1−u^2 +λ(1+u^2 ))) =∫ ((2du)/((λ−1)u^2 +1+λ)) =∫((−2du)/((1−λ)u^2 −(1+λ))) =((−2)/(1−λ)) ∫ (du/(u^2 −((1+λ)/(1−λ))))( look that ((1+λ)/(1−λ))>0) =_(u=(√((1+λ)/(1−λ)))z) ((−2)/(1−λ))((1−λ)/(1+λ)) ∫ (1/(z^2 −1))((√(1+λ))/( (√(1−λ))))dz =((−1)/( (√(1−λ^2 )))) ∫((1/(z−1))−(1/(z+1)))dz =((−1)/( (√(1−λ^2 ))))ln∣((z−1)/(z+1))∣ +C =((−1)/( (√(1−cos^2 (a−b))))) ×ln∣(((√((1−λ)/(1+λ)))tan((t/2))−1)/( (√((1−λ)/(1+λ)))tan((t/2))+1))∣ +C =((−1)/(∣sin(a−b)∣))×ln∣((tan(((a−b)/2))tan(x−((a+b)/2))−1)/(tan(((a−b)/2))tan(x−((a+b)/2))+1))∣ +C with a−b≠kπ k∈Z

$${let}\:{I}=\int\:\frac{{dx}}{{cos}\left({x}−{a}\right){cos}\left({x}−{b}\right)}\:\Rightarrow{I}=\int\:\:\frac{\mathrm{2}{dx}}{{cos}\left(\mathrm{2}{x}−{a}−{b}\right)+{cos}\left({a}−{b}\right)} \\ $$$$=_{\mathrm{2}{x}−\left({a}+{b}\right)={t}} \:\:\:\:\int\:\:\frac{{dt}}{{cost}\:+\lambda}\:\:{with}\:\lambda={cos}\left({a}−{b}\right)\:{changement} \\ $$$${tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}\:{give}\:\int\:\:\:\frac{{dt}}{{cost}\:+\lambda}\:=\int\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }+\lambda}\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\int\:\:\:\frac{\mathrm{2}{du}}{\mathrm{1}−{u}^{\mathrm{2}} \:+\lambda\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\int\:\:\frac{\mathrm{2}{du}}{\left(\lambda−\mathrm{1}\right){u}^{\mathrm{2}} +\mathrm{1}+\lambda}\:=\int\frac{−\mathrm{2}{du}}{\left(\mathrm{1}−\lambda\right){u}^{\mathrm{2}} −\left(\mathrm{1}+\lambda\right)} \\ $$$$=\frac{−\mathrm{2}}{\mathrm{1}−\lambda}\:\int\:\:\frac{{du}}{{u}^{\mathrm{2}} −\frac{\mathrm{1}+\lambda}{\mathrm{1}−\lambda}}\left(\:{look}\:{that}\:\frac{\mathrm{1}+\lambda}{\mathrm{1}−\lambda}>\mathrm{0}\right) \\ $$$$=_{{u}=\sqrt{\frac{\mathrm{1}+\lambda}{\mathrm{1}−\lambda}}{z}} \:\:\frac{−\mathrm{2}}{\mathrm{1}−\lambda}\frac{\mathrm{1}−\lambda}{\mathrm{1}+\lambda}\:\int\:\:\frac{\mathrm{1}}{{z}^{\mathrm{2}} −\mathrm{1}}\frac{\sqrt{\mathrm{1}+\lambda}}{\:\sqrt{\mathrm{1}−\lambda}}{dz} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\:\int\left(\frac{\mathrm{1}}{{z}−\mathrm{1}}−\frac{\mathrm{1}}{{z}+\mathrm{1}}\right){dz}\:=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}{ln}\mid\frac{{z}−\mathrm{1}}{{z}+\mathrm{1}}\mid\:+{C} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{1}−{cos}^{\mathrm{2}} \left({a}−{b}\right)}}\:×{ln}\mid\frac{\sqrt{\frac{\mathrm{1}−\lambda}{\mathrm{1}+\lambda}}{tan}\left(\frac{{t}}{\mathrm{2}}\right)−\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}−\lambda}{\mathrm{1}+\lambda}}{tan}\left(\frac{{t}}{\mathrm{2}}\right)+\mathrm{1}}\mid\:+{C} \\ $$$$=\frac{−\mathrm{1}}{\mid{sin}\left({a}−{b}\right)\mid}×{ln}\mid\frac{{tan}\left(\frac{{a}−{b}}{\mathrm{2}}\right){tan}\left({x}−\frac{{a}+{b}}{\mathrm{2}}\right)−\mathrm{1}}{{tan}\left(\frac{{a}−{b}}{\mathrm{2}}\right){tan}\left({x}−\frac{{a}+{b}}{\mathrm{2}}\right)+\mathrm{1}}\mid\:+{C}\:\:{with}\:{a}−{b}\neq{k}\pi\: \\ $$$${k}\in{Z}\: \\ $$$$ \\ $$

Commented by peter frank last updated on 20/Oct/19

$${thank}\:{you} \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 23/Oct/19

$${you}\:{are}\:{welcome}. \\ $$

Answered by Tanmay chaudhury last updated on 19/Oct/19

(1/(sin(a−b)))∫((sin{(x−b)−(x−a)})/(cos(x−a)cos(x−b)))dx (1/(sin(a−b)))∫((sin(x−b)cos(x−a)−cos(x−b)sin(x−a))/(cos(x−a)cos(x−b)))dx (1/(sin(a−b)))∫[tan(x−b)−tan(x−a)]dx (1/(sin(a−b)))[lnsec(x−b)−lnsec(x−a)]+c (1/(sin(a−b)))ln(((sec(x−b))/(sec(x−a))))+c

$$\frac{\mathrm{1}}{{sin}\left({a}−{b}\right)}\int\frac{{sin}\left\{\left({x}−{b}\right)−\left({x}−{a}\right)\right\}}{{cos}\left({x}−{a}\right){cos}\left({x}−{b}\right)}{dx} \\ $$$$\frac{\mathrm{1}}{{sin}\left({a}−{b}\right)}\int\frac{{sin}\left({x}−{b}\right){cos}\left({x}−{a}\right)−{cos}\left({x}−{b}\right){sin}\left({x}−{a}\right)}{{cos}\left({x}−{a}\right){cos}\left({x}−{b}\right)}{dx} \\ $$$$\frac{\mathrm{1}}{{sin}\left({a}−{b}\right)}\int\left[{tan}\left({x}−{b}\right)−{tan}\left({x}−{a}\right)\right]{dx} \\ $$$$\frac{\mathrm{1}}{{sin}\left({a}−{b}\right)}\left[{lnsec}\left({x}−{b}\right)−{lnsec}\left({x}−{a}\right)\right]+{c} \\ $$$$\frac{\mathrm{1}}{{sin}\left({a}−{b}\right)}{ln}\left(\frac{{sec}\left({x}−{b}\right)}{{sec}\left({x}−{a}\right)}\right)+{c} \\ $$

Commented by $@ty@m123 last updated on 19/Oct/19

$${Quite}\:{easier}\:{but}\:{tricky}. \\ $$

Commented by peter frank last updated on 19/Oct/19

$${thank}\:{you}\:{very}\:{much} \\ $$$$ \\ $$

Commented by Prithwish sen last updated on 19/Oct/19

tanmoy sir pujo kamon katlo. subho bijaya. kothae chilen ? bhalo achen ?

$$\mathrm{tanmoy}\:\mathrm{sir}\:\mathrm{pujo}\:\mathrm{kamon}\:\mathrm{katlo}.\:\mathrm{subho}\:\mathrm{bijaya}. \\ $$$$\mathrm{kothae}\:\mathrm{chilen}\:?\:\mathrm{bhalo}\:\mathrm{achen}\:? \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply