Menu Close

Question-71759

Tinku Tara 0 Comments
Pin




Question Number 71759 by naka3546 last updated on 19/Oct/19
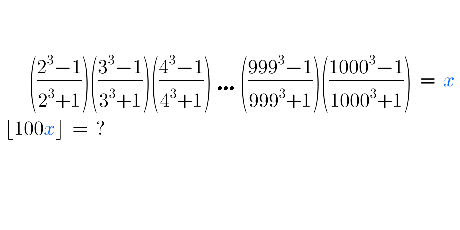
Commented by Prithwish sen last updated on 19/Oct/19
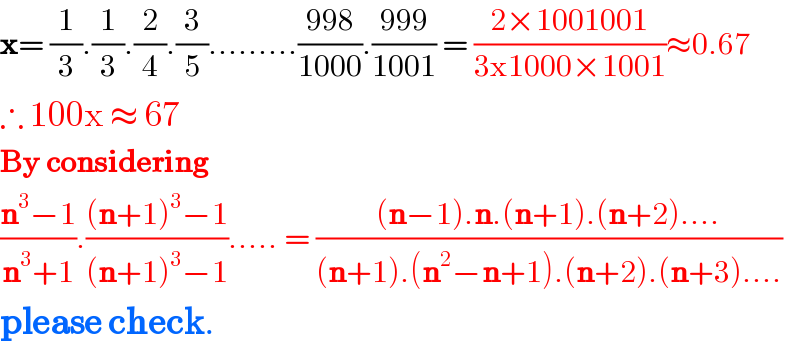
x= (1/3).(1/3).(2/4).(3/5).........((998)/(1000)).((999)/(1001)) = ((2×1001001)/(3x1000×1001))≈0.67 ∴ 100x ≈ 67 By considering ((n^3 −1)/(n^3 +1)).(((n+1)^3 −1)/((n+1)^3 −1))..... = (((n−1).n.(n+1).(n+2)....)/((n+1).(n^2 −n+1).(n+2).(n+3)....)) please check.
$$\boldsymbol{\mathrm{x}}=\:\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{2}}{\mathrm{4}}.\frac{\mathrm{3}}{\mathrm{5}}………\frac{\mathrm{998}}{\mathrm{1000}}.\frac{\mathrm{999}}{\mathrm{1001}}\:=\:\frac{\mathrm{2}×\mathrm{1001001}}{\mathrm{3×1000}×\mathrm{1001}}\approx\mathrm{0}.\mathrm{67} \\ $$$$\therefore\:\mathrm{100x}\:\approx\:\mathrm{67} \\ $$$$\boldsymbol{\mathrm{By}}\:\boldsymbol{\mathrm{considering}} \\ $$$$\frac{\boldsymbol{\mathrm{n}}^{\mathrm{3}} −\mathrm{1}}{\boldsymbol{\mathrm{n}}^{\mathrm{3}} +\mathrm{1}}.\frac{\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{1}}{\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{1}}…..\:=\:\frac{\left(\boldsymbol{\mathrm{n}}−\mathrm{1}\right).\boldsymbol{\mathrm{n}}.\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right).\left(\boldsymbol{\mathrm{n}}+\mathrm{2}\right)….}{\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right).\left(\boldsymbol{\mathrm{n}}^{\mathrm{2}} −\boldsymbol{\mathrm{n}}+\mathrm{1}\right).\left(\boldsymbol{\mathrm{n}}+\mathrm{2}\right).\left(\boldsymbol{\mathrm{n}}+\mathrm{3}\right)….} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Commented by Abdo msup. last updated on 20/Oct/19
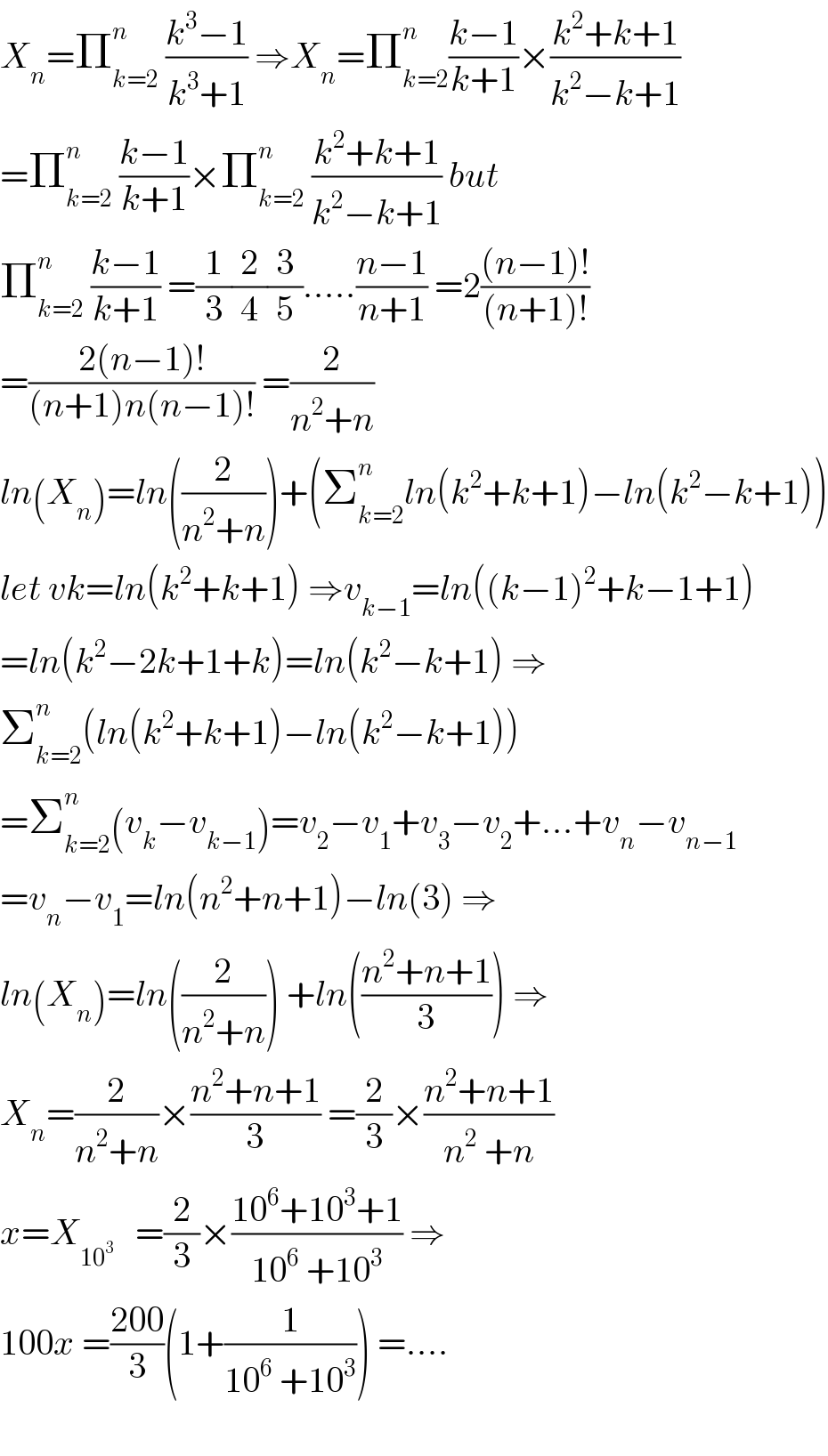
X_n =Π_(k=2) ^n ((k^3 −1)/(k^3 +1)) ⇒X_n =Π_(k=2) ^n ((k−1)/(k+1))×((k^2 +k+1)/(k^2 −k+1)) =Π_(k=2) ^n ((k−1)/(k+1))×Π_(k=2) ^n ((k^2 +k+1)/(k^2 −k+1)) but Π_(k=2) ^n ((k−1)/(k+1)) =(1/3)(2/4)(3/5).....((n−1)/(n+1)) =2(((n−1)!)/((n+1)!)) =((2(n−1)!)/((n+1)n(n−1)!)) =(2/(n^2 +n)) ln(X_n )=ln((2/(n^2 +n)))+(Σ_(k=2) ^n ln(k^2 +k+1)−ln(k^2 −k+1)) let vk=ln(k^2 +k+1) ⇒v_(k−1) =ln((k−1)^2 +k−1+1) =ln(k^2 −2k+1+k)=ln(k^2 −k+1) ⇒ Σ_(k=2) ^n (ln(k^2 +k+1)−ln(k^2 −k+1)) =Σ_(k=2) ^n (v_k −v_(k−1) )=v_2 −v_1 +v_3 −v_2 +...+v_n −v_(n−1) =v_n −v_1 =ln(n^2 +n+1)−ln(3) ⇒ ln(X_n )=ln((2/(n^2 +n))) +ln(((n^2 +n+1)/3)) ⇒ X_n =(2/(n^2 +n))×((n^2 +n+1)/3) =(2/3)×((n^2 +n+1)/(n^2 +n)) x=X_(10^3 ) =(2/3)×((10^6 +10^3 +1)/(10^6 +10^3 )) ⇒ 100x =((200)/3)(1+(1/(10^6 +10^3 ))) =....
$${X}_{{n}} =\prod_{{k}=\mathrm{2}} ^{{n}} \:\frac{{k}^{\mathrm{3}} −\mathrm{1}}{{k}^{\mathrm{3}} +\mathrm{1}}\:\Rightarrow{X}_{{n}} =\prod_{{k}=\mathrm{2}} ^{{n}} \frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}×\frac{{k}^{\mathrm{2}} +{k}+\mathrm{1}}{{k}^{\mathrm{2}} −{k}+\mathrm{1}} \\ $$$$=\prod_{{k}=\mathrm{2}} ^{{n}} \:\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}×\prod_{{k}=\mathrm{2}} ^{{n}} \:\frac{{k}^{\mathrm{2}} +{k}+\mathrm{1}}{{k}^{\mathrm{2}} −{k}+\mathrm{1}}\:{but} \\ $$$$\prod_{{k}=\mathrm{2}} ^{{n}} \:\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{3}}\frac{\mathrm{2}}{\mathrm{4}}\frac{\mathrm{3}}{\mathrm{5}}…..\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}\:=\mathrm{2}\frac{\left({n}−\mathrm{1}\right)!}{\left({n}+\mathrm{1}\right)!} \\ $$$$=\frac{\mathrm{2}\left({n}−\mathrm{1}\right)!}{\left({n}+\mathrm{1}\right){n}\left({n}−\mathrm{1}\right)!}\:=\frac{\mathrm{2}}{{n}^{\mathrm{2}} +{n}} \\ $$$${ln}\left({X}_{{n}} \right)={ln}\left(\frac{\mathrm{2}}{{n}^{\mathrm{2}} +{n}}\right)+\left(\sum_{{k}=\mathrm{2}} ^{{n}} {ln}\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)−{ln}\left({k}^{\mathrm{2}} −{k}+\mathrm{1}\right)\right) \\ $$$${let}\:{vk}={ln}\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)\:\Rightarrow{v}_{{k}−\mathrm{1}} ={ln}\left(\left({k}−\mathrm{1}\right)^{\mathrm{2}} +{k}−\mathrm{1}+\mathrm{1}\right) \\ $$$$={ln}\left({k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1}+{k}\right)={ln}\left({k}^{\mathrm{2}} −{k}+\mathrm{1}\right)\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{2}} ^{{n}} \left({ln}\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)−{ln}\left({k}^{\mathrm{2}} −{k}+\mathrm{1}\right)\right) \\ $$$$=\sum_{{k}=\mathrm{2}} ^{{n}} \left({v}_{{k}} −{v}_{{k}−\mathrm{1}} \right)={v}_{\mathrm{2}} −{v}_{\mathrm{1}} +{v}_{\mathrm{3}} −{v}_{\mathrm{2}} +…+{v}_{{n}} −{v}_{{n}−\mathrm{1}} \\ $$$$={v}_{{n}} −{v}_{\mathrm{1}} ={ln}\left({n}^{\mathrm{2}} +{n}+\mathrm{1}\right)−{ln}\left(\mathrm{3}\right)\:\Rightarrow \\ $$$${ln}\left({X}_{{n}} \right)={ln}\left(\frac{\mathrm{2}}{{n}^{\mathrm{2}} +{n}}\right)\:+{ln}\left(\frac{{n}^{\mathrm{2}} +{n}+\mathrm{1}}{\mathrm{3}}\right)\:\Rightarrow \\ $$$${X}_{{n}} =\frac{\mathrm{2}}{{n}^{\mathrm{2}} +{n}}×\frac{{n}^{\mathrm{2}} +{n}+\mathrm{1}}{\mathrm{3}}\:=\frac{\mathrm{2}}{\mathrm{3}}×\frac{{n}^{\mathrm{2}} +{n}+\mathrm{1}}{{n}^{\mathrm{2}} \:+{n}} \\ $$$${x}={X}_{\mathrm{10}^{\mathrm{3}} } \:\:\:=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{10}^{\mathrm{6}} +\mathrm{10}^{\mathrm{3}} +\mathrm{1}}{\mathrm{10}^{\mathrm{6}} \:+\mathrm{10}^{\mathrm{3}} }\:\Rightarrow \\ $$$$\mathrm{100}{x}\:=\frac{\mathrm{200}}{\mathrm{3}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{10}^{\mathrm{6}} \:+\mathrm{10}^{\mathrm{3}} }\right)\:=…. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *