Question-71776

Question Number 71776 by TawaTawa last updated on 19/Oct/19

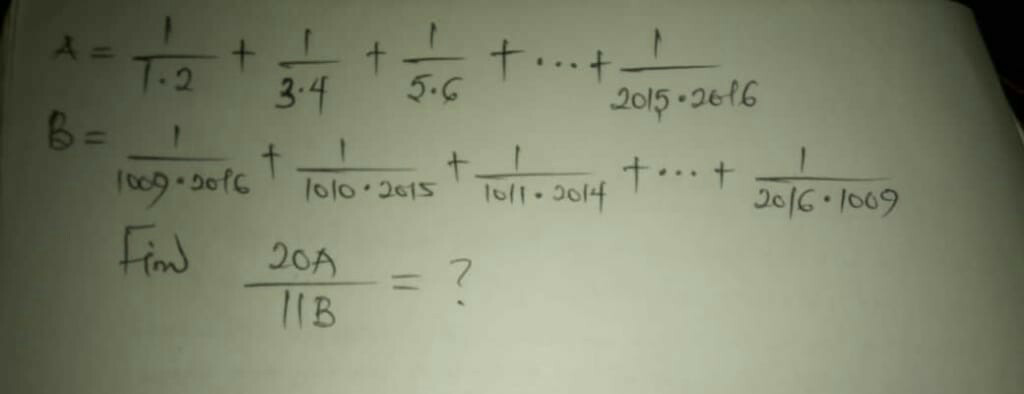
Answered by tw000001 last updated on 22/Oct/19

Use Harmonic series to solve. A=1−(1/2)+(1/3)−(1/4)+...+(1/(2015))−(1/(2016)) =(1+(1/2)+(1/3)+...+(1/(2016)))−2((1/2)+(1/4)+(1/6)+...+(1/(2016))) =(1+(1/2)+(1/3)+...+(1/(2016)))−(1+(1/2)+(1/3)+...+(1/(1008))) =H_(2016) −H_(1008) B=((2((1/(1009))+(1/(1010))+(1/(1011))+...+(1/(2016))))/(3025)) =((2(H_(2016) −H_(1008) ))/(3025))=((2A)/(3025)) ∴((20A)/(11B))=((20×3025)/(11×2))=2750

$$\mathrm{Use}\:\mathrm{Harmonic}\:\mathrm{series}\:\mathrm{to}\:\mathrm{solve}. \\ $$$${A}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+…+\frac{\mathrm{1}}{\mathrm{2015}}−\frac{\mathrm{1}}{\mathrm{2016}} \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{2016}}\right)−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{6}}+…+\frac{\mathrm{1}}{\mathrm{2016}}\right) \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{2016}}\right)−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{1008}}\right) \\ $$$$={H}_{\mathrm{2016}} −{H}_{\mathrm{1008}} \\ $$$${B}=\frac{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{1009}}+\frac{\mathrm{1}}{\mathrm{1010}}+\frac{\mathrm{1}}{\mathrm{1011}}+…+\frac{\mathrm{1}}{\mathrm{2016}}\right)}{\mathrm{3025}} \\ $$$$=\frac{\mathrm{2}\left({H}_{\mathrm{2016}} −{H}_{\mathrm{1008}} \right)}{\mathrm{3025}}=\frac{\mathrm{2}{A}}{\mathrm{3025}} \\ $$$$\therefore\frac{\mathrm{20}{A}}{\mathrm{11}{B}}=\frac{\mathrm{20}×\mathrm{3025}}{\mathrm{11}×\mathrm{2}}=\mathrm{2750} \\ $$

Commented by TawaTawa last updated on 22/Oct/19

Thanks for producing more steps, God bless you sir

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{producing}\:\mathrm{more}\:\mathrm{steps},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by TawaTawa last updated on 21/Oct/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time} \\ $$

Commented by TawaTawa last updated on 21/Oct/19

Somebody must have mistakenly flag instead of like. Thanks for the solution sir.

$$\mathrm{Somebody}\:\mathrm{must}\:\mathrm{have}\:\mathrm{mistakenly}\:\mathrm{flag}\:\mathrm{instead}\:\mathrm{of}\:\mathrm{like}. \\ $$$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{sir}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply