Question Number 71799 by mind is power last updated on 20/Oct/19
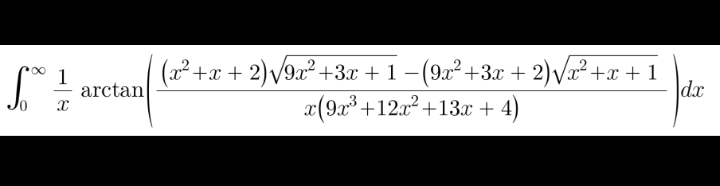
Answered by mind is power last updated on 20/Oct/19
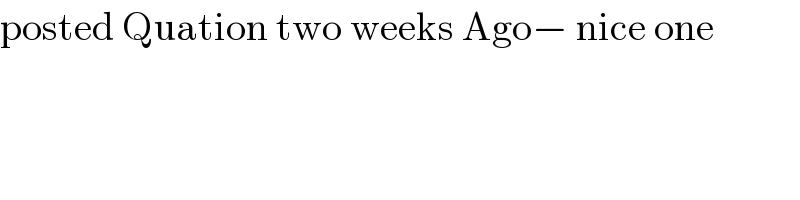
$$\mathrm{posted}\:\mathrm{Quation}\:\mathrm{two}\:\mathrm{weeks}\:\mathrm{Ago}−\:\mathrm{nice}\:\mathrm{one}\: \\ $$
Answered by mind is power last updated on 20/Oct/19
![(x^2 +x+2)(√(9x^2 +3x+1))−(9x^2 +3x+2)(√(x^2 +x+1)) =(√((x^2 +x+1)(9x^2 +3x+1)))((√(9x^2 +3x+1))−(√(x^2 +x+1)))+(√(9x^2 +3x+1))−(√(x^2 +x+1)) =((√(9x^2 +3x+1))−(√(x^2 +x+1))).((√((9x^2 +3x+1)(x^2 +x+1)))−1) =((((√(9x^2 +3x+1))−(√(x^2 +x+1)))(x(9x^3 +12x^2 +13x+4))/(((√((9x^2 +3x+1)(x^2 +x+1)+))1))) ⇒(((x^2 +x+2)(√(9x^2 +3x+1))−(9x^2 +3x+2)(√(x^2 +x+1)))/(x(9x^3 +12x^2 +13x+4)))=((−(√(9x^2 +3x+1+))(√(x^2 +x+1)))/((1+(√((9x^2 +3x+1)))((√(x^2 +x+1))))) ⇒arctg((((x^2 +x+2)(√(9x^2 +3x+1))−(9x^2 +3x+2)(√(x^2 +x+1)))/(x(9x^3 +12x^2 +13x+4))))=arctg(((−(√(9x^2 +3x+1+))(√(x^2 +x+1)))/((1+(√((9x^2 +3x+1)))((√(x^2 +x+1)))))) =arctg((√(x^2 +x+1)))−arctg((√(9x^2 +3x+1))) ⇒∫_0 ^(+∞) ((arctg((√(x^2 +x+1)))−arctg((√(9x^2 +3x+1)))/x) let f(x)=arctg((√(x^2 +x+1))) ⇒∫_0 ^(+∞) ((arctg((√(x^2 +x+1)))−arctg((√(9x^2 +3x+1)))/x)=∫_0 ^(+∞) ((f(1x)−f(3x))/x) ∫_0 ^(+∞) ((g(ax)−g(bx))/x)=∫_0 ^(+∞) ∫_b ^a g′(tx)dtdx=∫_b ^a (∫_0 ^(+∞) g′(tx)dx)dt =∫_b ^a [((g(tx))/t)]_0 ^(+∞) dt=(g(∞)−g(0)).∫_b ^a (dt/t)=(g(∞)−g(0))ln((a/b)) applie this gor f(x)=tan^(−1) ((√(x^2 +x+1))) f(0)=(π/4),lim f(x)=(π/2) ⇒∫_0 ^∞ ((f(1x)−f(3x))/x)dx=((π/2)−(π/4)).ln((1/3))=−((πln(3))/4)](https://www.tinkutara.com/question/Q71840.png)
$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{2}\right)\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}}−\left(\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{2}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}} \\ $$$$=\sqrt{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)\left(\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}\right)}\left(\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}}−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right)+\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}}−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}} \\ $$$$=\left(\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}}−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right).\left(\sqrt{\left(\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}−\mathrm{1}\right) \\ $$$$=\frac{\left(\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}}−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right)\left(\mathrm{x}\left(\mathrm{9x}^{\mathrm{3}} +\mathrm{12x}^{\mathrm{2}} +\mathrm{13x}+\mathrm{4}\right)\right.}{\left(\sqrt{\left(\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)+}\mathrm{1}\right)} \\ $$$$\Rightarrow\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{2}\right)\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}}−\left(\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{2}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}\left(\mathrm{9x}^{\mathrm{3}} +\mathrm{12x}^{\mathrm{2}} +\mathrm{13x}+\mathrm{4}\right)}=\frac{−\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}+}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\left(\mathrm{1}+\sqrt{\left(\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}\right.}\right)\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right)} \\ $$$$\Rightarrow\mathrm{arctg}\left(\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{2}\right)\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}}−\left(\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{2}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}\left(\mathrm{9x}^{\mathrm{3}} +\mathrm{12x}^{\mathrm{2}} +\mathrm{13x}+\mathrm{4}\right)}\right)=\mathrm{arctg}\left(\frac{−\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}+}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\left(\mathrm{1}+\sqrt{\left(\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}\right.}\right)\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right)}\right) \\ $$$$=\mathrm{arctg}\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right)−\mathrm{arctg}\left(\sqrt{\left.\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}\right)}\right. \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{arctg}\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right)−\mathrm{arctg}\left(\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}}\right.}{\mathrm{x}} \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{arctg}\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{arctg}\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right)−\mathrm{arctg}\left(\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{1}}\right.}{\mathrm{x}}=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{f}\left(\mathrm{1x}\right)−\mathrm{f}\left(\mathrm{3x}\right)}{\mathrm{x}} \\ $$$$\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{g}\left(\mathrm{ax}\right)−\mathrm{g}\left(\mathrm{bx}\right)}{\mathrm{x}}=\int_{\mathrm{0}} ^{+\infty} \int_{\mathrm{b}} ^{\mathrm{a}} \mathrm{g}'\left(\mathrm{tx}\right)\mathrm{dtdx}=\int_{\mathrm{b}} ^{\mathrm{a}} \left(\int_{\mathrm{0}} ^{+\infty} \mathrm{g}'\left(\mathrm{tx}\right)\mathrm{dx}\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{b}} ^{\mathrm{a}} \left[\frac{\mathrm{g}\left(\mathrm{tx}\right)}{\mathrm{t}}\right]_{\mathrm{0}} ^{+\infty} \mathrm{dt}=\left(\mathrm{g}\left(\infty\right)−\mathrm{g}\left(\mathrm{0}\right)\right).\int_{\mathrm{b}} ^{\mathrm{a}} \frac{\mathrm{dt}}{\mathrm{t}}=\left(\mathrm{g}\left(\infty\right)−\mathrm{g}\left(\mathrm{0}\right)\right)\mathrm{ln}\left(\frac{\mathrm{a}}{\mathrm{b}}\right) \\ $$$$\mathrm{applie}\:\mathrm{this}\:\mathrm{gor}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right) \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\frac{\pi}{\mathrm{4}},\mathrm{lim}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{f}\left(\mathrm{1x}\right)−\mathrm{f}\left(\mathrm{3x}\right)}{\mathrm{x}}\mathrm{dx}=\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right).\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=−\frac{\pi\mathrm{ln}\left(\mathrm{3}\right)}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
