Question Number 71868 by naka3546 last updated on 21/Oct/19
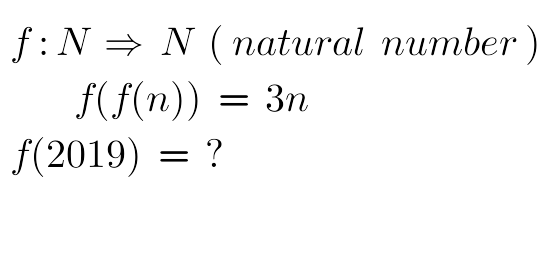
Commented by prakash jain last updated on 21/Oct/19

$${f}\left({n}\right)=\mathrm{0} \\ $$
Commented by mr W last updated on 21/Oct/19
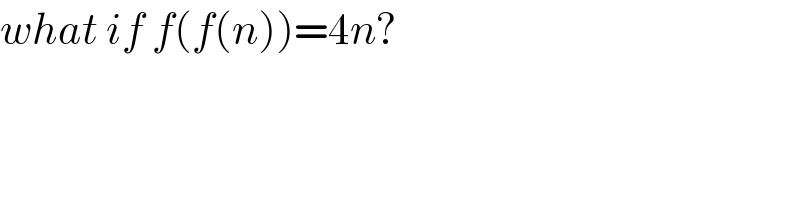
$${what}\:{if}\:{f}\left({f}\left({n}\right)\right)=\mathrm{4}{n}? \\ $$
Commented by Cmr 237 last updated on 21/Oct/19

$${premierement}\:{tu}\:{doit}\:{preciser} \\ $$$${que}\:{f}\:{est}\:{croissante}! \\ $$$${now}\:{we}\:{have}\:{prove}\:\:{that} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{2}\:{and}\:{f}\left(\mathrm{2}\right)=\mathrm{3} \\ $$$$\boldsymbol{{prove}}: \\ $$$${supposons}\:{que}\:{f}\left(\mathrm{1}\right)={k} \\ $$$$−{if}\:{k}<\mathrm{2}\:{we}\:{have}\: \\ $$$${f}\left(\mathrm{1}\right)<\mathrm{2}\:\Rightarrow{f}\left(\mathrm{1}\right)\leqslant\mathrm{1}\:{ie}\:{f}\searrow \\ $$$${absurde}\:{car}\:{f}\:\nearrow\:{par}\:{definition}. \\ $$$$−{if}\:{k}=\mathrm{3} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{3}\Rightarrow{f}\left({f}\left(\mathrm{1}\right)\right)={f}\left(\mathrm{3}\right)=\mathrm{3} \\ $$$${absurde}\:{car}\:{f}\:\nearrow \\ $$$$−{if}\:{k}>\mathrm{3}\:{we}\:{have} \\ $$$${f}\left({f}\left(\mathrm{1}\right)\right)={f}\left({k}\right)=\mathrm{3}\:{absurde}\:{car}\:{f}\nearrow \\ $$$${donc}\:{f}\left(\mathrm{1}\right)=\mathrm{2} \\ $$$${genalement},{pour}\:\mathrm{0}<{q}<\mathrm{3}^{{k}} \\ $$$${f}\left(\mathrm{3}^{{k}} +{q}\right)=\mathrm{2}×\mathrm{3}^{{k}} +{q}\:{et} \\ $$$${f}\left(\mathrm{2}×\mathrm{3}^{{k}} +{q}\right)=\mathrm{3}^{{k}+\mathrm{1}} +\mathrm{3}{q} \\ $$$$\mathrm{2019}=\mathrm{2}×\mathrm{3}^{\mathrm{6}} +\mathrm{561} \\ $$$${f}\left(\mathrm{2019}\right)=\mathrm{3}^{\mathrm{7}} +\mathrm{3}×\mathrm{561} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3870} \\ $$$$ \\ $$$$ \\ $$
