Menu Close

Question-71964

Tinku Tara 0 Comments
Pin




Question Number 71964 by mr W last updated on 22/Oct/19
Commented by mr W last updated on 22/Oct/19
find x=?
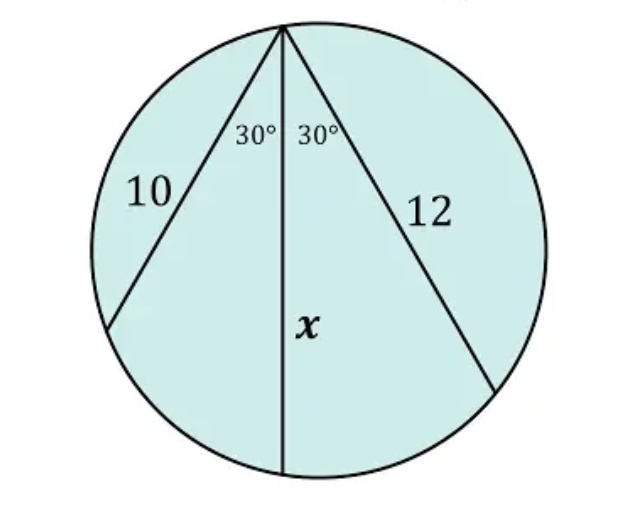
$${find}\:{x}=? \\ $$
Answered by behi83417@gmail.com last updated on 24/Oct/19
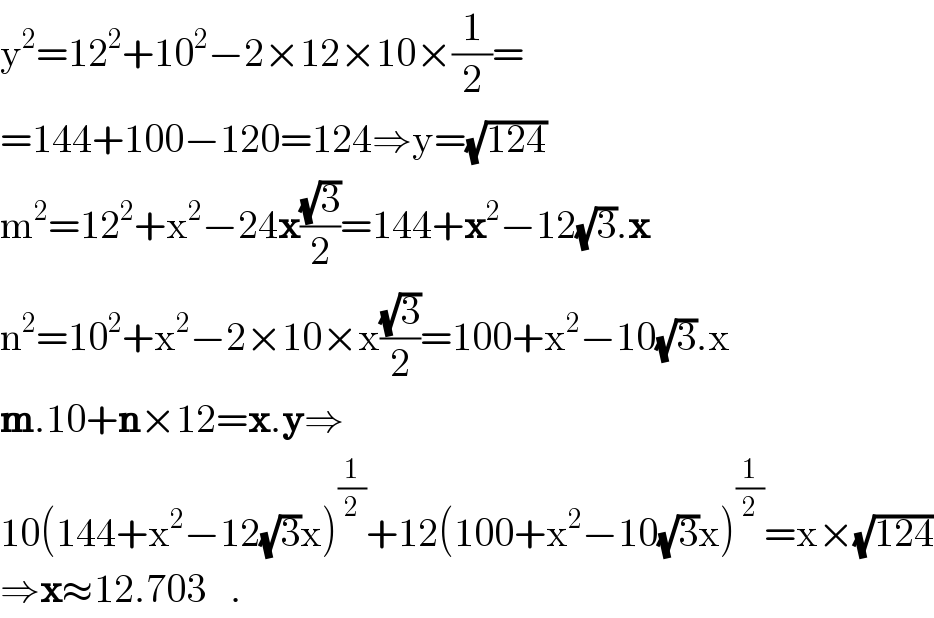
y^2 =12^2 +10^2 −2×12×10×(1/2)= =144+100−120=124⇒y=(√(124)) m^2 =12^2 +x^2 −24x((√3)/2)=144+x^2 −12(√3).x n^2 =10^2 +x^2 −2×10×x((√3)/2)=100+x^2 −10(√3).x m.10+n×12=x.y⇒ 10(144+x^2 −12(√3)x)^(1/2) +12(100+x^2 −10(√3)x)^(1/2) =x×(√(124)) ⇒x≈12.703 .
$$\mathrm{y}^{\mathrm{2}} =\mathrm{12}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} −\mathrm{2}×\mathrm{12}×\mathrm{10}×\frac{\mathrm{1}}{\mathrm{2}}= \\ $$$$=\mathrm{144}+\mathrm{100}−\mathrm{120}=\mathrm{124}\Rightarrow\mathrm{y}=\sqrt{\mathrm{124}} \\ $$$$\mathrm{m}^{\mathrm{2}} =\mathrm{12}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} −\mathrm{24}\boldsymbol{\mathrm{x}}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{144}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{12}\sqrt{\mathrm{3}}.\boldsymbol{\mathrm{x}} \\ $$$$\mathrm{n}^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} −\mathrm{2}×\mathrm{10}×\mathrm{x}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{100}+\mathrm{x}^{\mathrm{2}} −\mathrm{10}\sqrt{\mathrm{3}}.\mathrm{x} \\ $$$$\boldsymbol{\mathrm{m}}.\mathrm{10}+\boldsymbol{\mathrm{n}}×\mathrm{12}=\boldsymbol{\mathrm{x}}.\boldsymbol{\mathrm{y}}\Rightarrow \\ $$$$\mathrm{10}\left(\mathrm{144}+\mathrm{x}^{\mathrm{2}} −\mathrm{12}\sqrt{\mathrm{3}}\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{12}\left(\mathrm{100}+\mathrm{x}^{\mathrm{2}} −\mathrm{10}\sqrt{\mathrm{3}}\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{x}×\sqrt{\mathrm{124}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{x}}\approx\mathrm{12}.\mathrm{703}\:\:\:. \\ $$
Answered by mind is power last updated on 22/Oct/19
AB=12,AC=10 AD=x BC^2 =144+100−240cos(60)=244−120=124 BC=(√(124))=2(√(31)) ((AB.BC.AC)/(2S_(ABC) ))=2R S_(ABC) =((10.sin(60).12)/2)=30(√3) 2R=((10.12.2(√(31)))/(2.30(√3)))=((4(√(31)))/( (√3))) R=2(√((31)/3)) BD^2 =12^2 +x^2 −24xcos(30)=144+x^2 −12x(√3) S_(ABD) =((12xsin(30))/2)=3x ⇒4(√((31)/3))=((x.(√((x^2 −12x(√3)+144))).12)/(6x))=2(√(x^2 −12x(√3)+144)) ⇒4.((31)/3)=x^2 −12x(√3)+144 ⇒124=3x^2 −36(√3)x+432 ⇒3x^2 −36(√3)x+308=0 (3.36^2 )−12.308=3.1296−3696=3888−3696=192 x_1 =((36(√3)−(√(192)))/6)=((36(√3)−8(√3))/6)=4(√3) X_2 =((36(√3)+(√(192)))/6)=((44(√3))/6)=((22(√3))/3) x≥12⇒x=((22(√3))/3)
$$\mathrm{AB}=\mathrm{12},\mathrm{AC}=\mathrm{10} \\ $$$$\mathrm{AD}=\mathrm{x} \\ $$$$\mathrm{BC}^{\mathrm{2}} =\mathrm{144}+\mathrm{100}−\mathrm{240cos}\left(\mathrm{60}\right)=\mathrm{244}−\mathrm{120}=\mathrm{124} \\ $$$$\mathrm{BC}=\sqrt{\mathrm{124}}=\mathrm{2}\sqrt{\mathrm{31}} \\ $$$$\frac{\mathrm{AB}.\mathrm{BC}.\mathrm{AC}}{\mathrm{2S}_{\mathrm{ABC}} }=\mathrm{2R}\: \\ $$$$\mathrm{S}_{\mathrm{ABC}} =\frac{\mathrm{10}.\mathrm{sin}\left(\mathrm{60}\right).\mathrm{12}}{\mathrm{2}}=\mathrm{30}\sqrt{\mathrm{3}} \\ $$$$\mathrm{2R}=\frac{\mathrm{10}.\mathrm{12}.\mathrm{2}\sqrt{\mathrm{31}}}{\mathrm{2}.\mathrm{30}\sqrt{\mathrm{3}}}=\frac{\mathrm{4}\sqrt{\mathrm{31}}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{R}=\mathrm{2}\sqrt{\frac{\mathrm{31}}{\mathrm{3}}} \\ $$$$\mathrm{BD}^{\mathrm{2}} =\mathrm{12}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} −\mathrm{24xcos}\left(\mathrm{30}\right)=\mathrm{144}+\mathrm{x}^{\mathrm{2}} −\mathrm{12x}\sqrt{\mathrm{3}} \\ $$$$\mathrm{S}_{\mathrm{ABD}} =\frac{\mathrm{12xsin}\left(\mathrm{30}\right)}{\mathrm{2}}=\mathrm{3x} \\ $$$$\Rightarrow\mathrm{4}\sqrt{\frac{\mathrm{31}}{\mathrm{3}}}=\frac{\mathrm{x}.\sqrt{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{12x}\sqrt{\mathrm{3}}+\mathrm{144}\right)}.\mathrm{12}}{\mathrm{6x}}=\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{12x}\sqrt{\mathrm{3}}+\mathrm{144}} \\ $$$$\Rightarrow\mathrm{4}.\frac{\mathrm{31}}{\mathrm{3}}=\mathrm{x}^{\mathrm{2}} −\mathrm{12x}\sqrt{\mathrm{3}}+\mathrm{144} \\ $$$$\Rightarrow\mathrm{124}=\mathrm{3x}^{\mathrm{2}} −\mathrm{36}\sqrt{\mathrm{3}}\mathrm{x}+\mathrm{432} \\ $$$$\Rightarrow\mathrm{3x}^{\mathrm{2}} −\mathrm{36}\sqrt{\mathrm{3}}\mathrm{x}+\mathrm{308}=\mathrm{0} \\ $$$$\left(\mathrm{3}.\mathrm{36}^{\mathrm{2}} \right)−\mathrm{12}.\mathrm{308}=\mathrm{3}.\mathrm{1296}−\mathrm{3696}=\mathrm{3888}−\mathrm{3696}=\mathrm{192} \\ $$$$\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{36}\sqrt{\mathrm{3}}−\sqrt{\mathrm{192}}}{\mathrm{6}}=\frac{\mathrm{36}\sqrt{\mathrm{3}}−\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{6}}=\mathrm{4}\sqrt{\mathrm{3}} \\ $$$$\mathrm{X}_{\mathrm{2}} =\frac{\mathrm{36}\sqrt{\mathrm{3}}+\sqrt{\mathrm{192}}}{\mathrm{6}}=\frac{\mathrm{44}\sqrt{\mathrm{3}}}{\mathrm{6}}=\frac{\mathrm{22}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\mathrm{x}\geqslant\mathrm{12}\Rightarrow\mathrm{x}=\frac{\mathrm{22}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$ \\ $$
Commented by mr W last updated on 23/Oct/19
thanks sir! correct answer.
$${thanks}\:{sir}!\:{correct}\:{answer}. \\ $$
Commented by mind is power last updated on 23/Oct/19
y,re welcom
$$\mathrm{y},\mathrm{re}\:\mathrm{welcom} \\ $$
Answered by mr W last updated on 23/Oct/19
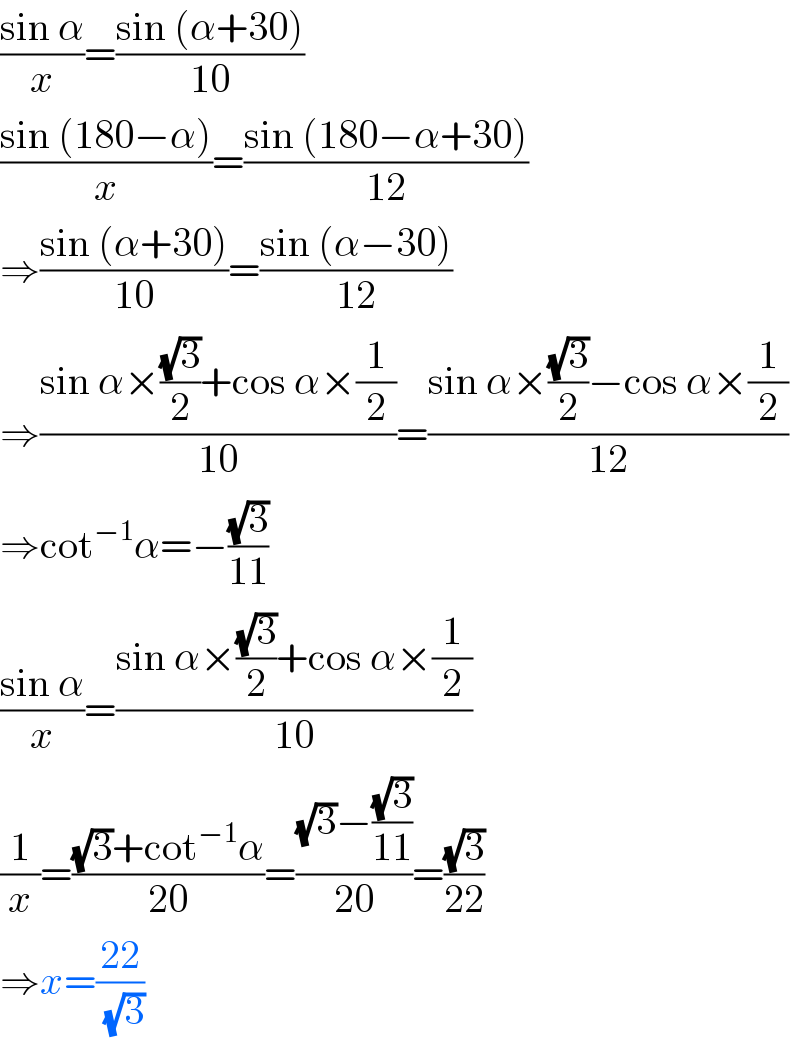
((sin α)/x)=((sin (α+30))/(10)) ((sin (180−α))/x)=((sin (180−α+30))/(12)) ⇒((sin (α+30))/(10))=((sin (α−30))/(12)) ⇒((sin α×((√3)/2)+cos α×(1/2))/(10))=((sin α×((√3)/2)−cos α×(1/2))/(12)) ⇒cot^(−1) α=−((√3)/(11)) ((sin α)/x)=((sin α×((√3)/2)+cos α×(1/2))/(10)) (1/x)=(((√3)+cot^(−1) α)/(20))=(((√3)−((√3)/(11)))/(20))=((√3)/(22)) ⇒x=((22)/( (√3)))
$$\frac{\mathrm{sin}\:\alpha}{{x}}=\frac{\mathrm{sin}\:\left(\alpha+\mathrm{30}\right)}{\mathrm{10}} \\ $$$$\frac{\mathrm{sin}\:\left(\mathrm{180}−\alpha\right)}{{x}}=\frac{\mathrm{sin}\:\left(\mathrm{180}−\alpha+\mathrm{30}\right)}{\mathrm{12}} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\left(\alpha+\mathrm{30}\right)}{\mathrm{10}}=\frac{\mathrm{sin}\:\left(\alpha−\mathrm{30}\right)}{\mathrm{12}} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\alpha×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\mathrm{cos}\:\alpha×\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{10}}=\frac{\mathrm{sin}\:\alpha×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{cos}\:\alpha×\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{12}} \\ $$$$\Rightarrow\mathrm{cot}^{−\mathrm{1}} \alpha=−\frac{\sqrt{\mathrm{3}}}{\mathrm{11}} \\ $$$$\frac{\mathrm{sin}\:\alpha}{{x}}=\frac{\mathrm{sin}\:\alpha×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\mathrm{cos}\:\alpha×\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{10}} \\ $$$$\frac{\mathrm{1}}{{x}}=\frac{\sqrt{\mathrm{3}}+\mathrm{cot}^{−\mathrm{1}} \alpha}{\mathrm{20}}=\frac{\sqrt{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{11}}}{\mathrm{20}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{22}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{22}}{\:\sqrt{\mathrm{3}}} \\ $$
Commented by mr W last updated on 23/Oct/19
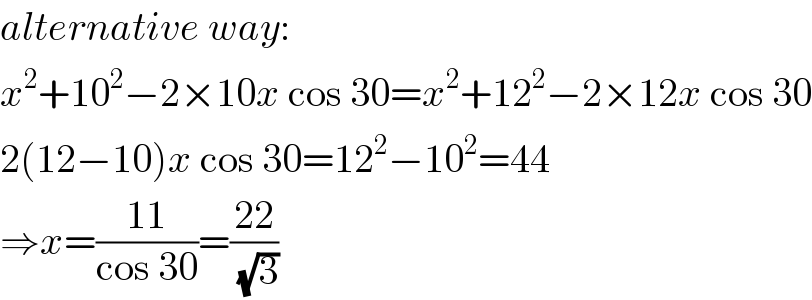
alternative way: x^2 +10^2 −2×10x cos 30=x^2 +12^2 −2×12x cos 30 2(12−10)x cos 30=12^2 −10^2 =44 ⇒x=((11)/(cos 30))=((22)/( (√3)))
$${alternative}\:{way}: \\ $$$${x}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} −\mathrm{2}×\mathrm{10}{x}\:\mathrm{cos}\:\mathrm{30}={x}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} −\mathrm{2}×\mathrm{12}{x}\:\mathrm{cos}\:\mathrm{30} \\ $$$$\mathrm{2}\left(\mathrm{12}−\mathrm{10}\right){x}\:\mathrm{cos}\:\mathrm{30}=\mathrm{12}^{\mathrm{2}} −\mathrm{10}^{\mathrm{2}} =\mathrm{44} \\ $$$$\Rightarrow{x}=\frac{\mathrm{11}}{\mathrm{cos}\:\mathrm{30}}=\frac{\mathrm{22}}{\:\sqrt{\mathrm{3}}} \\ $$
Commented by ajfour last updated on 23/Oct/19
the best!
$${the}\:{best}! \\ $$
Commented by mind is power last updated on 23/Oct/19
nice sir
$$\mathrm{nice}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 23/Oct/19
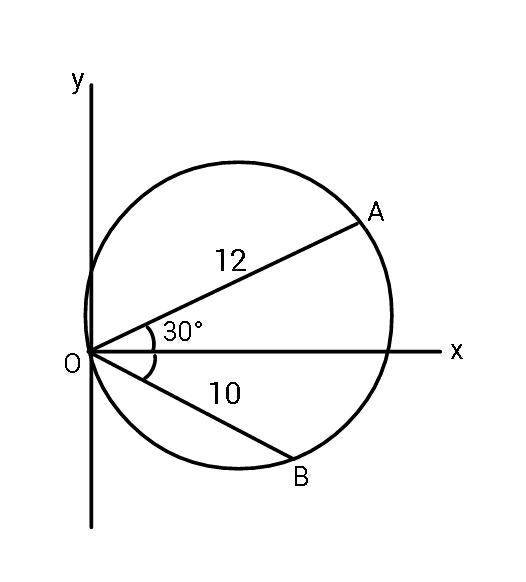
Commented by ajfour last updated on 23/Oct/19
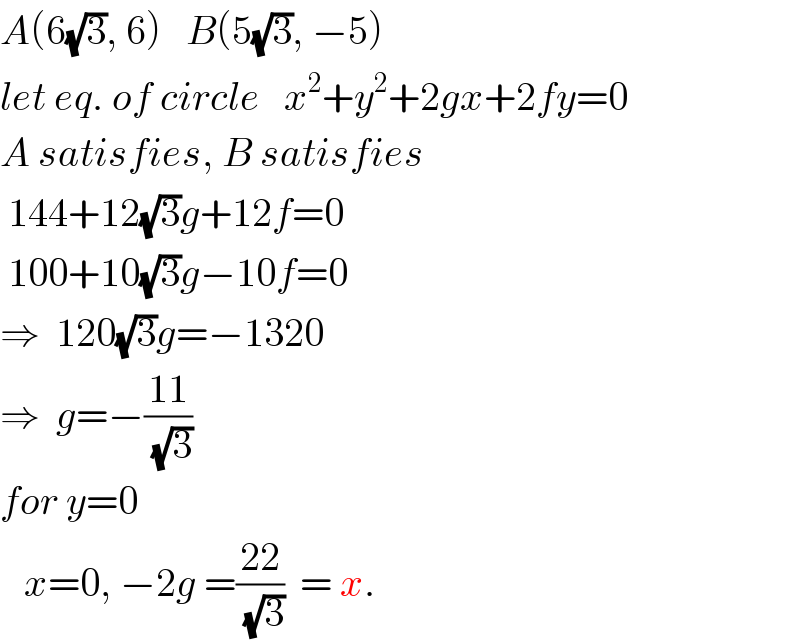
A(6(√3), 6) B(5(√3), −5) let eq. of circle x^2 +y^2 +2gx+2fy=0 A satisfies, B satisfies 144+12(√3)g+12f=0 100+10(√3)g−10f=0 ⇒ 120(√3)g=−1320 ⇒ g=−((11)/( (√3))) for y=0 x=0, −2g =((22)/( (√3))) = x.
$${A}\left(\mathrm{6}\sqrt{\mathrm{3}},\:\mathrm{6}\right)\:\:\:{B}\left(\mathrm{5}\sqrt{\mathrm{3}},\:−\mathrm{5}\right) \\ $$$${let}\:{eq}.\:{of}\:{circle}\:\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{gx}+\mathrm{2}{fy}=\mathrm{0} \\ $$$${A}\:{satisfies},\:{B}\:{satisfies} \\ $$$$\:\mathrm{144}+\mathrm{12}\sqrt{\mathrm{3}}{g}+\mathrm{12}{f}=\mathrm{0} \\ $$$$\:\mathrm{100}+\mathrm{10}\sqrt{\mathrm{3}}{g}−\mathrm{10}{f}=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{120}\sqrt{\mathrm{3}}{g}=−\mathrm{1320} \\ $$$$\Rightarrow\:\:{g}=−\frac{\mathrm{11}}{\:\sqrt{\mathrm{3}}} \\ $$$${for}\:{y}=\mathrm{0} \\ $$$$\:\:\:{x}=\mathrm{0},\:−\mathrm{2}{g}\:=\frac{\mathrm{22}}{\:\sqrt{\mathrm{3}}}\:\:=\:{x}. \\ $$
Commented by mind is power last updated on 23/Oct/19
nice solution sir
$$\mathrm{nice}\:\mathrm{solution}\:\mathrm{sir} \\ $$
Answered by john santu last updated on 19/Jan/20
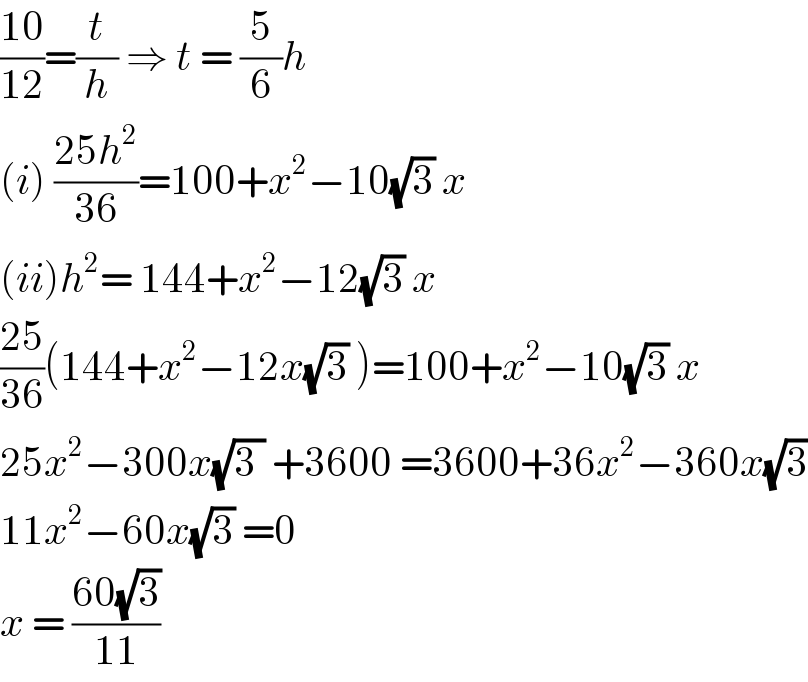
((10)/(12))=(t/h) ⇒ t = (5/6)h (i) ((25h^2 )/(36))=100+x^2 −10(√3) x (ii)h^2 = 144+x^2 −12(√3) x ((25)/(36))(144+x^2 −12x(√3) )=100+x^2 −10(√3) x 25x^2 −300x(√(3 )) +3600 =3600+36x^2 −360x(√3) 11x^2 −60x(√3) =0 x = ((60(√3))/(11))
$$\frac{\mathrm{10}}{\mathrm{12}}=\frac{{t}}{{h}}\:\Rightarrow\:{t}\:=\:\frac{\mathrm{5}}{\mathrm{6}}{h} \\ $$$$\left({i}\right)\:\frac{\mathrm{25}{h}^{\mathrm{2}} }{\mathrm{36}}=\mathrm{100}+{x}^{\mathrm{2}} −\mathrm{10}\sqrt{\mathrm{3}}\:{x} \\ $$$$\left({ii}\right){h}^{\mathrm{2}} =\:\mathrm{144}+{x}^{\mathrm{2}} −\mathrm{12}\sqrt{\mathrm{3}}\:{x} \\ $$$$\frac{\mathrm{25}}{\mathrm{36}}\left(\mathrm{144}+{x}^{\mathrm{2}} −\mathrm{12}{x}\sqrt{\mathrm{3}}\:\right)=\mathrm{100}+{x}^{\mathrm{2}} −\mathrm{10}\sqrt{\mathrm{3}}\:{x} \\ $$$$\mathrm{25}{x}^{\mathrm{2}} −\mathrm{300}{x}\sqrt{\mathrm{3}\:}\:+\mathrm{3600}\:=\mathrm{3600}+\mathrm{36}{x}^{\mathrm{2}} −\mathrm{360}{x}\sqrt{\mathrm{3}} \\ $$$$\mathrm{11}{x}^{\mathrm{2}} −\mathrm{60}{x}\sqrt{\mathrm{3}}\:=\mathrm{0} \\ $$$${x}\:=\:\frac{\mathrm{60}\sqrt{\mathrm{3}}}{\mathrm{11}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *