Question Number 72036 by mr W last updated on 23/Oct/19
Commented by mr W last updated on 23/Oct/19
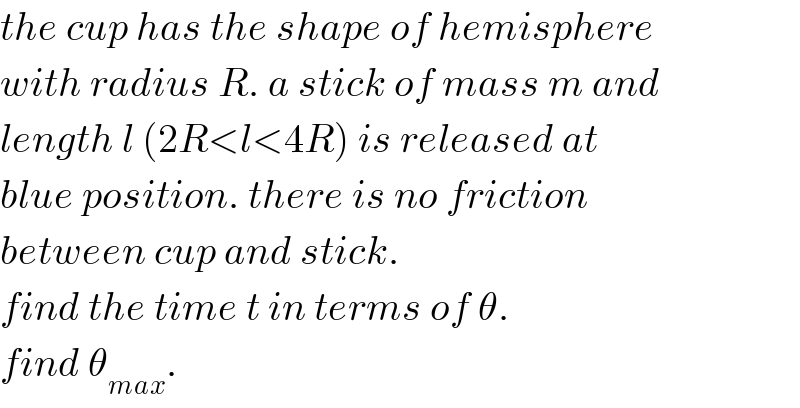
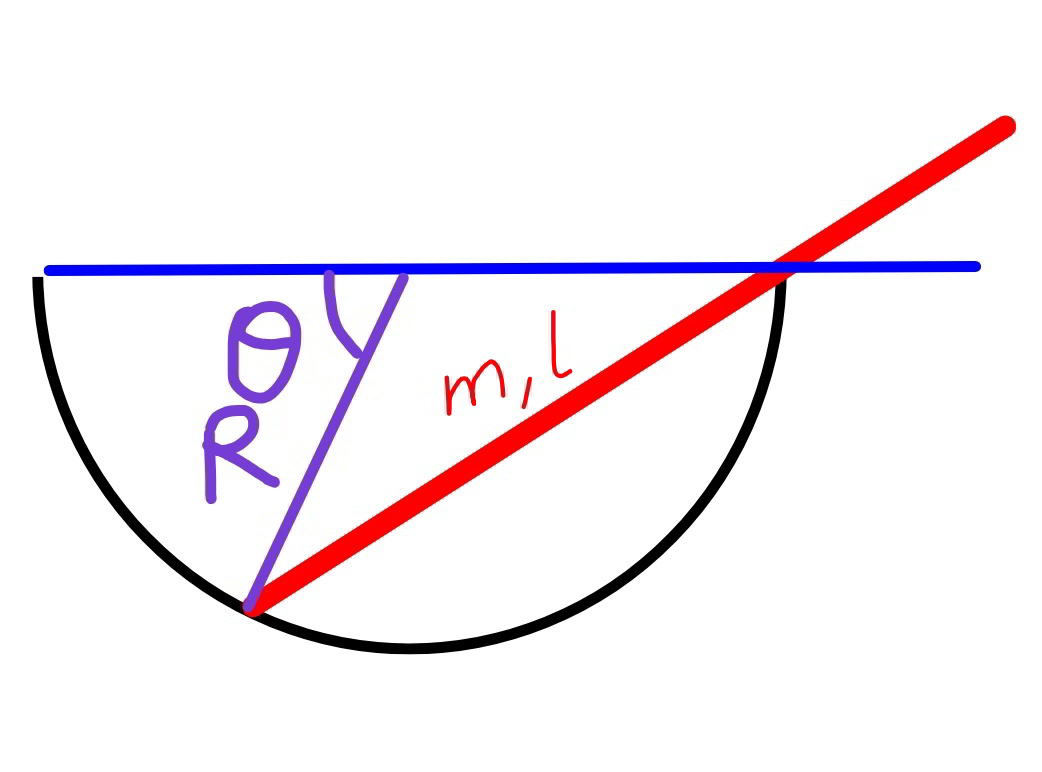
$${the}\:{cup}\:{has}\:{the}\:{shape}\:{of}\:{hemisphere} \\ $$$${with}\:{radius}\:{R}.\:{a}\:{stick}\:{of}\:{mass}\:{m}\:{and} \\ $$$${length}\:{l}\:\left(\mathrm{2}{R}<{l}<\mathrm{4}{R}\right)\:{is}\:{released}\:{at} \\ $$$${blue}\:{position}.\:{there}\:{is}\:{no}\:{friction} \\ $$$${between}\:{cup}\:{and}\:{stick}. \\ $$$${find}\:{the}\:{time}\:{t}\:{in}\:{terms}\:{of}\:\theta. \\ $$$${find}\:\theta_{{max}} . \\ $$
Commented by ajfour last updated on 23/Oct/19
$${cup}\:{fixed},\:{i}\:{guess}\:? \\ $$
Commented by mr W last updated on 23/Oct/19

$${yes}\:{sir}. \\ $$
Answered by mr W last updated on 24/Oct/19
Commented by mr W last updated on 24/Oct/19
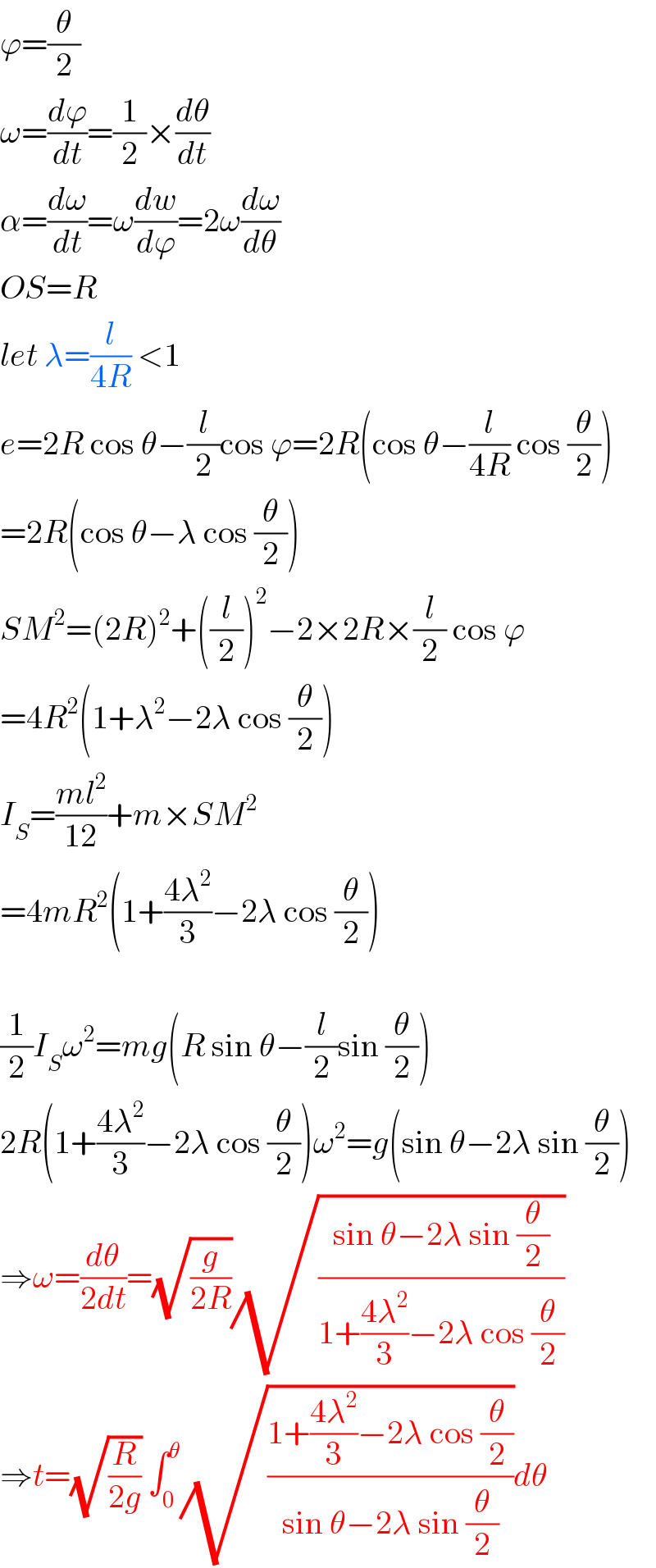
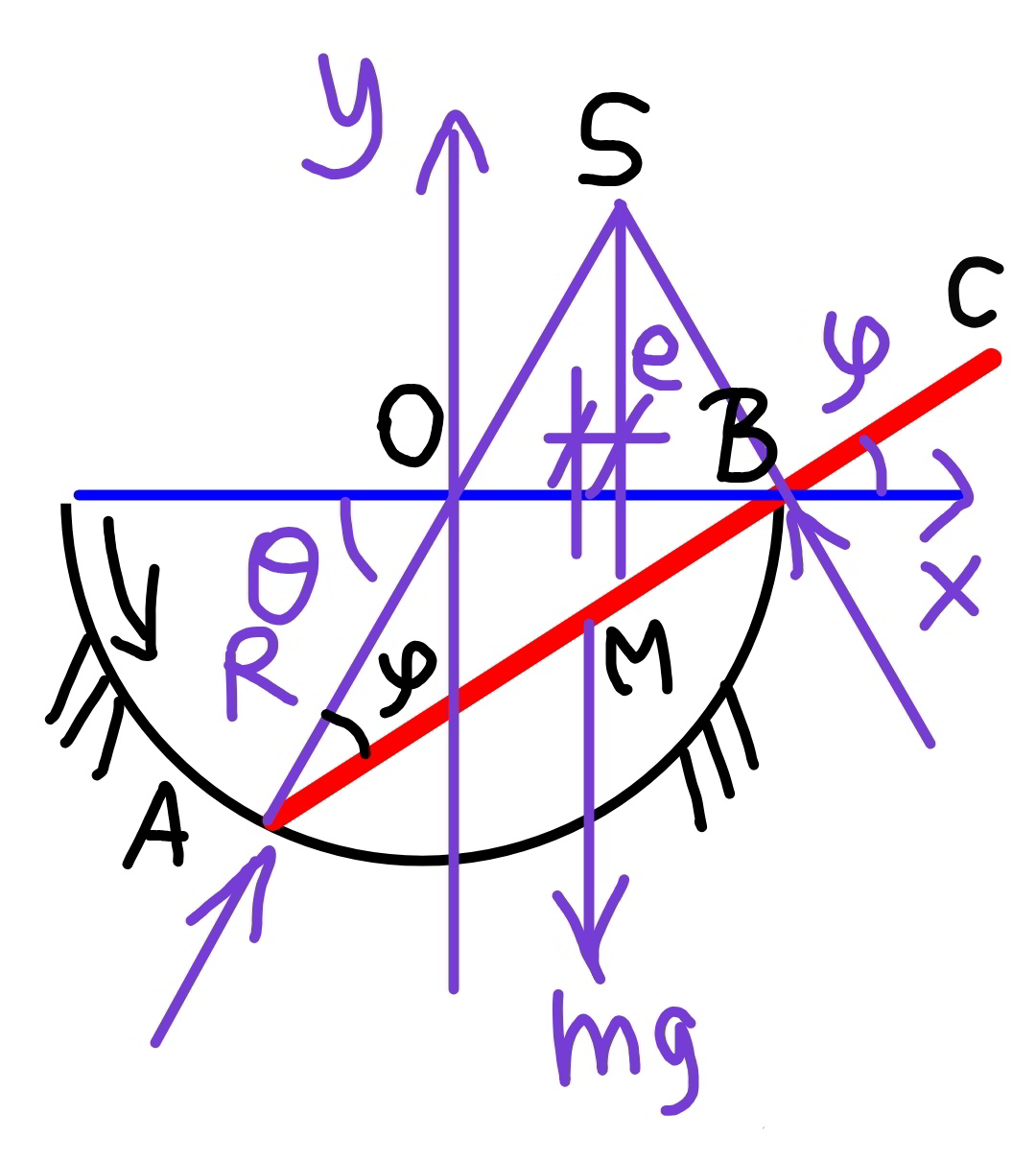
$$\varphi=\frac{\theta}{\mathrm{2}} \\ $$$$\omega=\frac{{d}\varphi}{{dt}}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{d}\theta}{{dt}} \\ $$$$\alpha=\frac{{d}\omega}{{dt}}=\omega\frac{{dw}}{{d}\varphi}=\mathrm{2}\omega\frac{{d}\omega}{{d}\theta} \\ $$$${OS}={R} \\ $$$${let}\:\lambda=\frac{{l}}{\mathrm{4}{R}}\:<\mathrm{1} \\ $$$${e}=\mathrm{2}{R}\:\mathrm{cos}\:\theta−\frac{{l}}{\mathrm{2}}\mathrm{cos}\:\varphi=\mathrm{2}{R}\left(\mathrm{cos}\:\theta−\frac{{l}}{\mathrm{4}{R}}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}{R}\left(\mathrm{cos}\:\theta−\lambda\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\right) \\ $$$${SM}^{\mathrm{2}} =\left(\mathrm{2}{R}\right)^{\mathrm{2}} +\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{2}{R}×\frac{{l}}{\mathrm{2}}\:\mathrm{cos}\:\varphi \\ $$$$=\mathrm{4}{R}^{\mathrm{2}} \left(\mathrm{1}+\lambda^{\mathrm{2}} −\mathrm{2}\lambda\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\right) \\ $$$${I}_{{S}} =\frac{{ml}^{\mathrm{2}} }{\mathrm{12}}+{m}×{SM}^{\mathrm{2}} \\ $$$$=\mathrm{4}{mR}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{4}\lambda^{\mathrm{2}} }{\mathrm{3}}−\mathrm{2}\lambda\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{I}_{{S}} \omega^{\mathrm{2}} ={mg}\left({R}\:\mathrm{sin}\:\theta−\frac{{l}}{\mathrm{2}}\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\right) \\ $$$$\mathrm{2}{R}\left(\mathrm{1}+\frac{\mathrm{4}\lambda^{\mathrm{2}} }{\mathrm{3}}−\mathrm{2}\lambda\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\right)\omega^{\mathrm{2}} ={g}\left(\mathrm{sin}\:\theta−\mathrm{2}\lambda\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\right) \\ $$$$\Rightarrow\omega=\frac{{d}\theta}{\mathrm{2}{dt}}=\sqrt{\frac{{g}}{\mathrm{2}{R}}}\sqrt{\frac{\mathrm{sin}\:\theta−\mathrm{2}\lambda\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}+\frac{\mathrm{4}\lambda^{\mathrm{2}} }{\mathrm{3}}−\mathrm{2}\lambda\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}}} \\ $$$$\Rightarrow{t}=\sqrt{\frac{{R}}{\mathrm{2}{g}}}\:\int_{\mathrm{0}} ^{\theta} \sqrt{\frac{\mathrm{1}+\frac{\mathrm{4}\lambda^{\mathrm{2}} }{\mathrm{3}}−\mathrm{2}\lambda\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}}{\mathrm{sin}\:\theta−\mathrm{2}\lambda\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}}{d}\theta \\ $$
Commented by ajfour last updated on 24/Oct/19
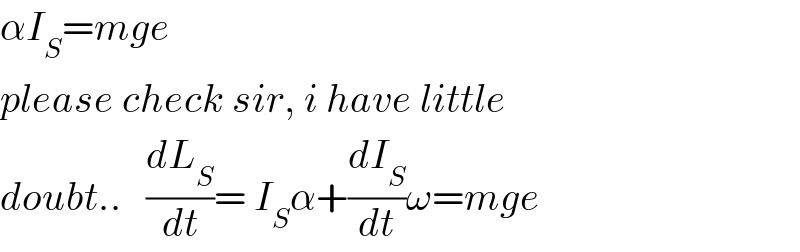
$$\alpha{I}_{{S}} ={mge} \\ $$$${please}\:{check}\:{sir},\:{i}\:{have}\:{little} \\ $$$${doubt}..\:\:\:\frac{{dL}_{{S}} }{{dt}}=\:{I}_{{S}} \alpha+\frac{{dI}_{{S}} }{{dt}}\omega={mge} \\ $$
Commented by mr W last updated on 24/Oct/19

$${you}\:{are}\:{very}\:{right}\:{sir}!\:{it}\:{is}\:{a}\: \\ $$$${system}\:{with}\:{variable}\:{MoI}. \\ $$$${but} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{I}_{{S}} \omega^{\mathrm{2}} ={mg}\Delta{h} \\ $$$${should}\:{be}\:{ok}. \\ $$
Commented by ajfour last updated on 24/Oct/19
$${yes}\:{i}\:{too}\:{think}\:{the}\:{other}\:{one}\:{okay}. \\ $$
Commented by mr W last updated on 24/Oct/19

$${thanks}\:{alot}\:{sir}! \\ $$
Answered by ajfour last updated on 23/Oct/19
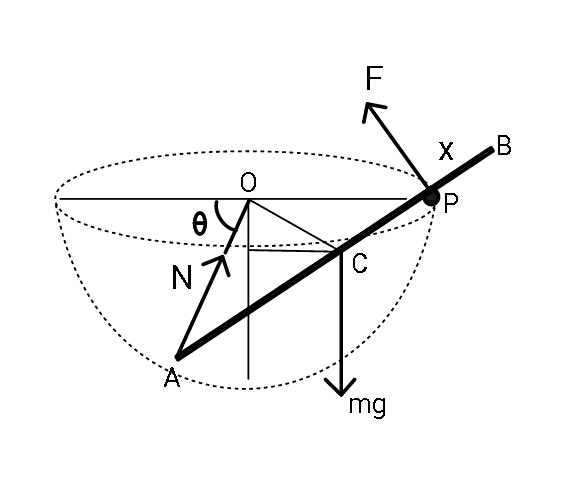
Commented by ajfour last updated on 24/Oct/19
 ..(iii) x=l−2Rcos φ ⇒ −(dx/dt)=−ωRsin φ (d^2 x/dt^2 )=ω^2 Rcos φ Now from (ii) Ncos φ−mgsin φ=m(d^2 x/dt^2 )+mω^2 ((l/2)−x) ⇒ N=mgtan φ+mω^2 R+mω^2 ((l/2)−x)sec φ using this and (i), (iii) in (dL/dt)=τ_P ⇒ 2ωm((l/2)−x)(−(dx/dt))+[((ml^2 )/(12))+m((l/2)−x)^2 ](dω/dt) =−(Nsin φ)(l−x)+(mgcos φ)((l/2)−x) ⇒ 2ω(2Rcos φ−(l/2))(−ωRsin φ) +[(l^2 /(12))+(2Rcos φ)^2 ]((ωdω)/dφ) = −{gtan φ+ω^2 R+ω^2 (2Rcos φ−(l/2))sec φ}sin φ(2Rcos φ) +gcos φ(2Rcos φ−(l/2)) ⇒ ((l^2 /(12))+4R^2 cos^2 φ)((ωdω)/dφ) +2ω^2 R^2 sin φcos φ = 2gR(cos^2 φ−sin^2 φ)−((glcos φ)/2) let ω^2 =z ⇒ (dz/dφ)+(((4R^2 sin φcos φ)/((l^2 /(12))+4R^2 cos^2 φ)))z = ((4gR(cos^2 φ−sin^2 φ)−glcos φ)/(l^2 /12+4R^2 cos^2 φ)) e^(∫Pdx) =e^(∫((4R^2 sin φcos φdφ)/(l^2 /12+4R^2 cos^2 φ))) =−(1/( (√(l^2 /12+4R^2 cos^2 φ)))) ⇒ −(z/( (√(l^2 /12+4R^2 cos^2 φ)))) =∫(([4gR(cos^2 φ−sin^2 φ)−glcos φ]dφ)/((l^2 /12+4R^2 cos^2 φ)^(3/2) )) .....](https://www.tinkutara.com/question/Q72096.png)
$${AP}\:=\mathrm{2}{R}\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\:\:\:\:\:;\:\:{x}={l}−\mathrm{2}{R}\mathrm{cos}\:\frac{\theta}{\mathrm{2}} \\ $$$${let}\:\phi=\frac{\theta}{\mathrm{2}} \\ $$$$\tau_{{P}} =−\left({N}\mathrm{sin}\:\phi\right)\left({l}−{x}\right)+\left({mg}\mathrm{cos}\:\phi\right)\left(\frac{{l}}{\mathrm{2}}−{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..\left({i}\right) \\ $$$${Also}\:{along}\:{rod} \\ $$$$\:{N}\mathrm{cos}\:\phi−{mg}\mathrm{sin}\:\phi={m}\frac{{d}^{\mathrm{2}} {x}}{{dt}^{\mathrm{2}} }+{m}\omega^{\mathrm{2}} \left(\frac{{l}}{\mathrm{2}}−{x}\right)\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……..\left({ii}\right) \\ $$$${L}={I}_{{P}} \:\omega\:\:\:{let}\:\:\omega=\frac{{d}\phi}{{dt}}=\frac{{d}\left(\theta/\mathrm{2}\right)}{{dt}} \\ $$$${I}_{{P}} =\frac{{ml}^{\mathrm{2}} }{\mathrm{12}}+{m}\left(\frac{{l}}{\mathrm{2}}−{x}\right)^{\mathrm{2}} \\ $$$$\frac{{dL}}{{dt}}=\mathrm{2}\omega{m}\left(\frac{{l}}{\mathrm{2}}−{x}\right)\left(−\frac{{dx}}{{dt}}\right)+ \\ $$$$\:\:\:\:\:\:\:\:\left[\frac{{ml}^{\mathrm{2}} }{\mathrm{2}}+{m}\left(\frac{{l}}{\mathrm{2}}−{x}\right)^{\mathrm{2}} \right]\frac{{d}\omega}{{dt}}\:\:\:..\left({iii}\right) \\ $$$$\:\:{x}={l}−\mathrm{2}{R}\mathrm{cos}\:\phi \\ $$$$\Rightarrow\:−\frac{{dx}}{{dt}}=−\omega{R}\mathrm{sin}\:\phi \\ $$$$\:\:\:\:\:\frac{{d}^{\mathrm{2}} {x}}{{dt}^{\mathrm{2}} }=\omega^{\mathrm{2}} {R}\mathrm{cos}\:\phi \\ $$$${Now}\:{from}\:\left({ii}\right) \\ $$$$\:{N}\mathrm{cos}\:\phi−{mg}\mathrm{sin}\:\phi={m}\frac{{d}^{\mathrm{2}} {x}}{{dt}^{\mathrm{2}} }+{m}\omega^{\mathrm{2}} \left(\frac{{l}}{\mathrm{2}}−{x}\right) \\ $$$$\Rightarrow\:{N}={mg}\mathrm{tan}\:\phi+{m}\omega^{\mathrm{2}} {R}+{m}\omega^{\mathrm{2}} \left(\frac{{l}}{\mathrm{2}}−{x}\right)\mathrm{sec}\:\phi \\ $$$${using}\:{this}\:{and}\:\left({i}\right),\:\left({iii}\right)\:{in} \\ $$$$\:\:\:\frac{{dL}}{{dt}}=\tau_{{P}} \:\:\:\Rightarrow \\ $$$$\mathrm{2}\omega{m}\left(\frac{{l}}{\mathrm{2}}−{x}\right)\left(−\frac{{dx}}{{dt}}\right)+\left[\frac{{ml}^{\mathrm{2}} }{\mathrm{12}}+{m}\left(\frac{{l}}{\mathrm{2}}−{x}\right)^{\mathrm{2}} \right]\frac{{d}\omega}{{dt}} \\ $$$$=−\left({N}\mathrm{sin}\:\phi\right)\left({l}−{x}\right)+\left({mg}\mathrm{cos}\:\phi\right)\left(\frac{{l}}{\mathrm{2}}−{x}\right) \\ $$$$\Rightarrow \\ $$$$\mathrm{2}\omega\left(\mathrm{2}{R}\mathrm{cos}\:\phi−\frac{{l}}{\mathrm{2}}\right)\left(−\omega{R}\mathrm{sin}\:\phi\right) \\ $$$$+\left[\frac{{l}^{\mathrm{2}} }{\mathrm{12}}+\left(\mathrm{2}{R}\mathrm{cos}\:\phi\right)^{\mathrm{2}} \right]\frac{\omega{d}\omega}{{d}\phi}\:= \\ $$$$\:\:−\left\{{g}\mathrm{tan}\:\phi+\omega^{\mathrm{2}} {R}+\omega^{\mathrm{2}} \left(\mathrm{2}{R}\mathrm{cos}\:\phi−\frac{{l}}{\mathrm{2}}\right)\mathrm{sec}\:\phi\right\}\mathrm{sin}\:\phi\left(\mathrm{2}{R}\mathrm{cos}\:\phi\right) \\ $$$$\:\:\:\:+{g}\mathrm{cos}\:\phi\left(\mathrm{2}{R}\mathrm{cos}\:\phi−\frac{{l}}{\mathrm{2}}\right) \\ $$$$\Rightarrow \\ $$$$\left(\frac{{l}^{\mathrm{2}} }{\mathrm{12}}+\mathrm{4}{R}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi\right)\frac{\omega{d}\omega}{{d}\phi} \\ $$$$\:\:+\mathrm{2}\omega^{\mathrm{2}} {R}^{\mathrm{2}} \mathrm{sin}\:\phi\mathrm{cos}\:\phi\:= \\ $$$$\:\:\:\:\:\mathrm{2}{gR}\left(\mathrm{cos}\:^{\mathrm{2}} \phi−\mathrm{sin}\:^{\mathrm{2}} \phi\right)−\frac{{gl}\mathrm{cos}\:\phi}{\mathrm{2}} \\ $$$${let}\:\:\omega^{\mathrm{2}} ={z}\:\:\Rightarrow \\ $$$$\frac{{dz}}{{d}\phi}+\left(\frac{\mathrm{4}{R}^{\mathrm{2}} \mathrm{sin}\:\phi\mathrm{cos}\:\phi}{\frac{{l}^{\mathrm{2}} }{\mathrm{12}}+\mathrm{4}{R}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi}\right){z} \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{\mathrm{4}{gR}\left(\mathrm{cos}\:^{\mathrm{2}} \phi−\mathrm{sin}\:^{\mathrm{2}} \phi\right)−{gl}\mathrm{cos}\:\phi}{{l}^{\mathrm{2}} /\mathrm{12}+\mathrm{4}{R}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi} \\ $$$${e}^{\int{Pdx}} ={e}^{\int\frac{\mathrm{4}{R}^{\mathrm{2}} \mathrm{sin}\:\phi\mathrm{cos}\:\phi{d}\phi}{{l}^{\mathrm{2}} /\mathrm{12}+\mathrm{4}{R}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi}} \\ $$$$\:\:\:\:=−\frac{\mathrm{1}}{\:\sqrt{{l}^{\mathrm{2}} /\mathrm{12}+\mathrm{4}{R}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi}} \\ $$$$\Rightarrow\:−\frac{{z}}{\:\sqrt{{l}^{\mathrm{2}} /\mathrm{12}+\mathrm{4}{R}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi}} \\ $$$$\:\:\:\:=\int\frac{\left[\mathrm{4}{gR}\left(\mathrm{cos}\:^{\mathrm{2}} \phi−\mathrm{sin}\:^{\mathrm{2}} \phi\right)−{gl}\mathrm{cos}\:\phi\right]{d}\phi}{\left({l}^{\mathrm{2}} /\mathrm{12}+\mathrm{4}{R}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi\right)^{\mathrm{3}/\mathrm{2}} } \\ $$$$….. \\ $$
