Menu Close

Question-72047

Tinku Tara 0 Comments
Pin




Question Number 72047 by aliesam last updated on 23/Oct/19
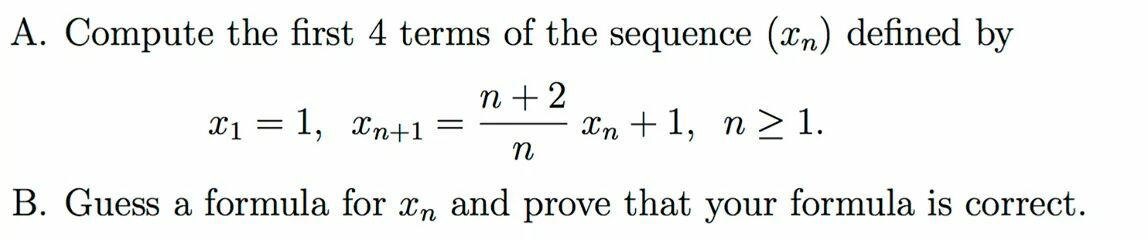
Commented by mind is power last updated on 23/Oct/19
x_1 =1,x_2 =4,x_3 =9,x_4 =16 ∀_n ∈N^∗ ,X_n =n^2 for n=1 we have X_1 =1=1^2 lets assume ∀n∈N^∗ x_n =n^2 X_(n+1) =((n+2)/n).n^2 +1=n^2 +2n+1=(n+1)^2 ⇒∀_n ∈N^∗ x_n =n^2 2nd x_n =U_n +p(n) U_(n+1) +p(n+1)=((n+2)/n).(u_n +p(n))+1 p(n+1)=(((n+2)/n))p(n)+1 ⇒np(n+1)=(n+2)p(n)+n p(n)=an+b ⇒n(a(n+1)+b)=(n+2)(an+b)+n ⇒an^2 +n(a+b)=an^2 +(b+2a+1)n+2b b=0 ,a=−1 p(n)=−n ⇒U_(n+1) =((n+2)/n)u_n ⇒(u_(n+1) /u_n )=((n+2)/n)⇒Π_(k=1) ^(n−1) (u_(n+1) /u_n )=Π_(k=1) ^(n−1) ((n+2)/n) Π_(k=1) ^(n−1) (u_(k+1) /u_k )=(u_2 /u_1 ).(u_3 /u_2 )....(u_n /u_(n−1) )=(u_n /u_1 ) Π_(k=1) ^(n−1) ((n+2)/n)=(3/1).(4/2).(5/3).(6/4).....((n+1)/n)=(((n)(n+1))/(1.2)) ⇒u_n =u_1 .(((n+1)(n))/2) X_n =u_n +p(n)=⇒u_1 +p(1)=x_1 =1⇒u_1 −1=1⇒u_1 =2 ⇒u_n =(n+1)(n)=n^2 +n x_n =u_n +p(n)=n^2 +n−n=n^2
$$\mathrm{x}_{\mathrm{1}} =\mathrm{1},\mathrm{x}_{\mathrm{2}} =\mathrm{4},\mathrm{x}_{\mathrm{3}} =\mathrm{9},\mathrm{x}_{\mathrm{4}} =\mathrm{16} \\ $$$$\forall_{\mathrm{n}} \in\mathbb{N}^{\ast} ,\mathrm{X}_{\mathrm{n}} =\mathrm{n}^{\mathrm{2}} \\ $$$$\mathrm{for}\:\mathrm{n}=\mathrm{1}\:\mathrm{we}\:\mathrm{have}\:\mathrm{X}_{\mathrm{1}} =\mathrm{1}=\mathrm{1}^{\mathrm{2}} \\ $$$$\mathrm{lets}\:\mathrm{assume}\:\forall\mathrm{n}\in\mathbb{N}^{\ast} \:\mathrm{x}_{\mathrm{n}} =\mathrm{n}^{\mathrm{2}} \\ $$$$\mathrm{X}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{n}+\mathrm{2}}{\mathrm{n}}.\mathrm{n}^{\mathrm{2}} +\mathrm{1}=\mathrm{n}^{\mathrm{2}} +\mathrm{2n}+\mathrm{1}=\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \Rightarrow\forall_{\mathrm{n}} \in\mathbb{N}\:^{\ast} \:\mathrm{x}_{\mathrm{n}} =\mathrm{n}^{\mathrm{2}} \\ $$$$\mathrm{2nd}\: \\ $$$$\mathrm{x}_{\mathrm{n}} =\mathrm{U}_{\mathrm{n}} +\mathrm{p}\left(\mathrm{n}\right) \\ $$$$\mathrm{U}_{\mathrm{n}+\mathrm{1}} +\mathrm{p}\left(\mathrm{n}+\mathrm{1}\right)=\frac{\mathrm{n}+\mathrm{2}}{\mathrm{n}}.\left(\mathrm{u}_{\mathrm{n}} +\mathrm{p}\left(\mathrm{n}\right)\right)+\mathrm{1} \\ $$$$\mathrm{p}\left(\mathrm{n}+\mathrm{1}\right)=\left(\frac{\mathrm{n}+\mathrm{2}}{\mathrm{n}}\right)\mathrm{p}\left(\mathrm{n}\right)+\mathrm{1} \\ $$$$\Rightarrow\mathrm{np}\left(\mathrm{n}+\mathrm{1}\right)=\left(\mathrm{n}+\mathrm{2}\right)\mathrm{p}\left(\mathrm{n}\right)+\mathrm{n} \\ $$$$\mathrm{p}\left(\mathrm{n}\right)=\mathrm{an}+\mathrm{b} \\ $$$$\Rightarrow\mathrm{n}\left(\mathrm{a}\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{b}\right)=\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{an}+\mathrm{b}\right)+\mathrm{n} \\ $$$$\Rightarrow\mathrm{an}^{\mathrm{2}} +\mathrm{n}\left(\mathrm{a}+\mathrm{b}\right)=\mathrm{an}^{\mathrm{2}} +\left(\mathrm{b}+\mathrm{2a}+\mathrm{1}\right)\mathrm{n}+\mathrm{2b} \\ $$$$\mathrm{b}=\mathrm{0}\:,\mathrm{a}=−\mathrm{1} \\ $$$$\mathrm{p}\left(\mathrm{n}\right)=−\mathrm{n} \\ $$$$\Rightarrow\mathrm{U}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{n}+\mathrm{2}}{\mathrm{n}}\mathrm{u}_{\mathrm{n}} \\ $$$$\Rightarrow\frac{\mathrm{u}_{\mathrm{n}+\mathrm{1}} }{\mathrm{u}_{\mathrm{n}} }=\frac{\mathrm{n}+\mathrm{2}}{\mathrm{n}}\Rightarrow\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\prod}}\frac{\mathrm{u}_{\mathrm{n}+\mathrm{1}} }{\mathrm{u}_{\mathrm{n}} }=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\prod}}\frac{\mathrm{n}+\mathrm{2}}{\mathrm{n}} \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\prod}}\frac{\mathrm{u}_{\mathrm{k}+\mathrm{1}} }{\mathrm{u}_{\mathrm{k}} }=\frac{\mathrm{u}_{\mathrm{2}} }{\mathrm{u}_{\mathrm{1}} }.\frac{\mathrm{u}_{\mathrm{3}} }{\mathrm{u}_{\mathrm{2}} }….\frac{\mathrm{u}_{\mathrm{n}} }{\mathrm{u}_{\mathrm{n}−\mathrm{1}} }=\frac{\mathrm{u}_{\mathrm{n}} }{\mathrm{u}_{\mathrm{1}} } \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\prod}}\frac{\mathrm{n}+\mathrm{2}}{\mathrm{n}}=\frac{\mathrm{3}}{\mathrm{1}}.\frac{\mathrm{4}}{\mathrm{2}}.\frac{\mathrm{5}}{\mathrm{3}}.\frac{\mathrm{6}}{\mathrm{4}}…..\frac{\mathrm{n}+\mathrm{1}}{\mathrm{n}}=\frac{\left(\mathrm{n}\right)\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{1}.\mathrm{2}} \\ $$$$\Rightarrow\mathrm{u}_{\mathrm{n}} =\mathrm{u}_{\mathrm{1}} .\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}\right)}{\mathrm{2}} \\ $$$$\mathrm{X}_{\mathrm{n}} =\mathrm{u}_{\mathrm{n}} +\mathrm{p}\left(\mathrm{n}\right)=\Rightarrow\mathrm{u}_{\mathrm{1}} +\mathrm{p}\left(\mathrm{1}\right)=\mathrm{x}_{\mathrm{1}} =\mathrm{1}\Rightarrow\mathrm{u}_{\mathrm{1}} −\mathrm{1}=\mathrm{1}\Rightarrow\mathrm{u}_{\mathrm{1}} =\mathrm{2} \\ $$$$\Rightarrow\mathrm{u}_{\mathrm{n}} =\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}\right)=\mathrm{n}^{\mathrm{2}} +\mathrm{n} \\ $$$$\mathrm{x}_{\mathrm{n}} =\mathrm{u}_{\mathrm{n}} +\mathrm{p}\left(\mathrm{n}\right)=\mathrm{n}^{\mathrm{2}} +\mathrm{n}−\mathrm{n}=\mathrm{n}^{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *