Question-72048

Question Number 72048 by ahmadshahhimat775@gmail.com last updated on 23/Oct/19

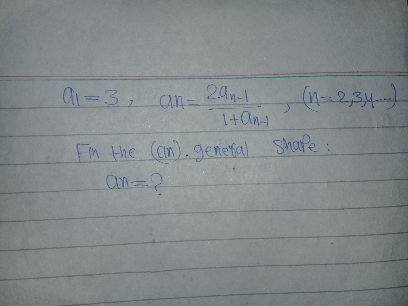
Answered by mind is power last updated on 23/Oct/19

a_2 =(6/(1+3))=(3/2)=((3.2^0 )/2)=((2+1)/2)=((2+2^0 )/2) a_3 =(3/(1+(3/2)))=(6/5) =((3.2)/(3.2−1))=((4+2)/(4+2−1))=((2+2^2 )/(2+2^2 −1)) a_4 =(((12)/5)/((11)/5))=((12)/(11))=((3.2^2 )/(3.2^2 −1))=((2^3 +2^2 )/(2^3 +2^2 −1)) a_5 =((24)/(23))=((3.2^3 )/(3.2^3 −1))=((2^4 +2^3 )/(2^4 +2^3 −1)) a_n =((2^(n−1) +2^(n−2) )/(2^(n−1) +2^(n−2) +1)) if n≥2 a_1 =3 assum a_n =((2^(n−1) +2^(n−2) )/(2^(n−1) +2^(n−2) −1)),a_(n+1) =((2^(n+1−1) +2^(n+1−2) )/(2^(n+1−1) +2^(n+1−2) −1))? a_(n+1) =((2.((2^(n−1) +2^(n−2) )/(2^(n−1) +2^(n−2) −1)))/(1+((2^(n−1) +2^(n−2) )/(2^(n−1) +2^(n−2) −1))))=((((2^(n+1−1) +2^(n+1−2) )/(2^(n−1) +2^(n−2) −1)) )/((2^(n−1) +2^(n−1) +2^(n−2) +2^(n−2) −1)/(2^(n−1) +2^(n−2) −1))) =((2^(n+1−1) +2^(n+1−2) )/(2^(n+1−1) +2^(n+1−2) −1))

$$\mathrm{a}_{\mathrm{2}} =\frac{\mathrm{6}}{\mathrm{1}+\mathrm{3}}=\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{3}.\mathrm{2}^{\mathrm{0}} }{\mathrm{2}}=\frac{\mathrm{2}+\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{2}+\mathrm{2}^{\mathrm{0}} }{\mathrm{2}} \\ $$$$\mathrm{a}_{\mathrm{3}} =\frac{\mathrm{3}}{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}}=\frac{\mathrm{6}}{\mathrm{5}}\:=\frac{\mathrm{3}.\mathrm{2}}{\mathrm{3}.\mathrm{2}−\mathrm{1}}=\frac{\mathrm{4}+\mathrm{2}}{\mathrm{4}+\mathrm{2}−\mathrm{1}}=\frac{\mathrm{2}+\mathrm{2}^{\mathrm{2}} }{\mathrm{2}+\mathrm{2}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{a}_{\mathrm{4}} =\frac{\frac{\mathrm{12}}{\mathrm{5}}}{\frac{\mathrm{11}}{\mathrm{5}}}=\frac{\mathrm{12}}{\mathrm{11}}=\frac{\mathrm{3}.\mathrm{2}^{\mathrm{2}} }{\mathrm{3}.\mathrm{2}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{a}_{\mathrm{5}} =\frac{\mathrm{24}}{\mathrm{23}}=\frac{\mathrm{3}.\mathrm{2}^{\mathrm{3}} }{\mathrm{3}.\mathrm{2}^{\mathrm{3}} −\mathrm{1}}=\frac{\mathrm{2}^{\mathrm{4}} +\mathrm{2}^{\mathrm{3}} }{\mathrm{2}^{\mathrm{4}} +\mathrm{2}^{\mathrm{3}} −\mathrm{1}} \\ $$$$\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{2}^{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}−\mathrm{2}} }{\mathrm{2}^{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}−\mathrm{2}} +\mathrm{1}}\:\mathrm{if}\:\mathrm{n}\geqslant\mathrm{2} \\ $$$$\mathrm{a}_{\mathrm{1}} =\mathrm{3} \\ $$$$\mathrm{assum}\:\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{2}^{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}−\mathrm{2}} }{\mathrm{2}^{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}},\mathrm{a}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{2}^{\mathrm{n}+\mathrm{1}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}+\mathrm{1}−\mathrm{2}} }{\mathrm{2}^{\mathrm{n}+\mathrm{1}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}+\mathrm{1}−\mathrm{2}} −\mathrm{1}}? \\ $$$$\mathrm{a}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{2}.\frac{\mathrm{2}^{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}−\mathrm{2}} }{\mathrm{2}^{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}}}{\mathrm{1}+\frac{\mathrm{2}^{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}−\mathrm{2}} }{\mathrm{2}^{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}}}=\frac{\frac{\mathrm{2}^{\mathrm{n}+\mathrm{1}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}+\mathrm{1}−\mathrm{2}} \:}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}}\:\:}{\frac{\mathrm{2}^{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}−\mathrm{2}} +\mathrm{2}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}}} \\ $$$$=\frac{\mathrm{2}^{\mathrm{n}+\mathrm{1}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}+\mathrm{1}−\mathrm{2}} }{\mathrm{2}^{\mathrm{n}+\mathrm{1}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}+\mathrm{1}−\mathrm{2}} −\mathrm{1}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply