Question Number 72108 by ajfour last updated on 24/Oct/19

Answered by Tanmay chaudhury last updated on 24/Oct/19
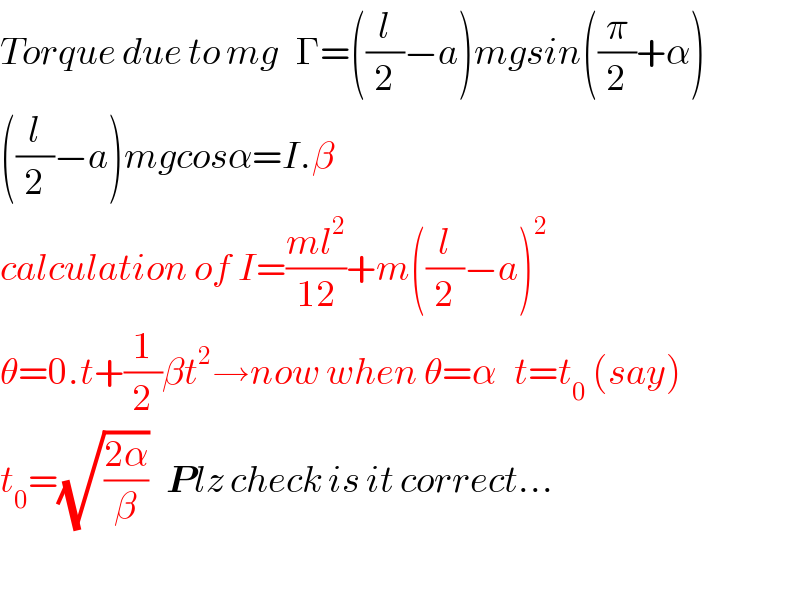
$${Torque}\:{due}\:{to}\:{mg}\:\:\:\Gamma=\left(\frac{{l}}{\mathrm{2}}−{a}\right){mgsin}\left(\frac{\pi}{\mathrm{2}}+\alpha\right) \\ $$$$\left(\frac{{l}}{\mathrm{2}}−{a}\right){mgcos}\alpha={I}.\beta \\ $$$${calculation}\:{of}\:{I}=\frac{{ml}^{\mathrm{2}} }{\mathrm{12}}+{m}\left(\frac{{l}}{\mathrm{2}}−{a}\right)^{\mathrm{2}} \\ $$$$\theta=\mathrm{0}.{t}+\frac{\mathrm{1}}{\mathrm{2}}\beta{t}^{\mathrm{2}} \rightarrow{now}\:{when}\:\theta=\alpha\:\:\:{t}={t}_{\mathrm{0}} \:\left({say}\right) \\ $$$${t}_{\mathrm{0}} =\sqrt{\frac{\mathrm{2}\alpha}{\beta}}\:\:\:\boldsymbol{{P}}{lz}\:{check}\:{is}\:{it}\:{correct}… \\ $$$$ \\ $$
Commented by Tanmay chaudhury last updated on 24/Oct/19

$${ok}\:{i}\:{shall}\:{go}\:{deep}\:{into}\left[{the}\:{problem}…\right. \\ $$
Commented by ajfour last updated on 24/Oct/19
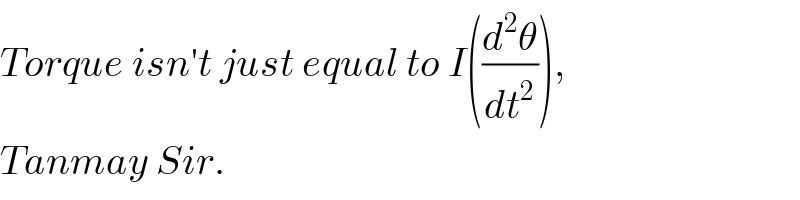
$${Torque}\:{isn}'{t}\:{just}\:{equal}\:{to}\:{I}\left(\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }\right), \\ $$$${Tanmay}\:{Sir}. \\ $$
