Question Number 72112 by A8;15: last updated on 24/Oct/19
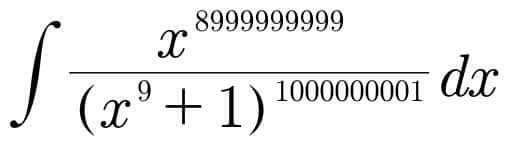
Answered by mind is power last updated on 24/Oct/19
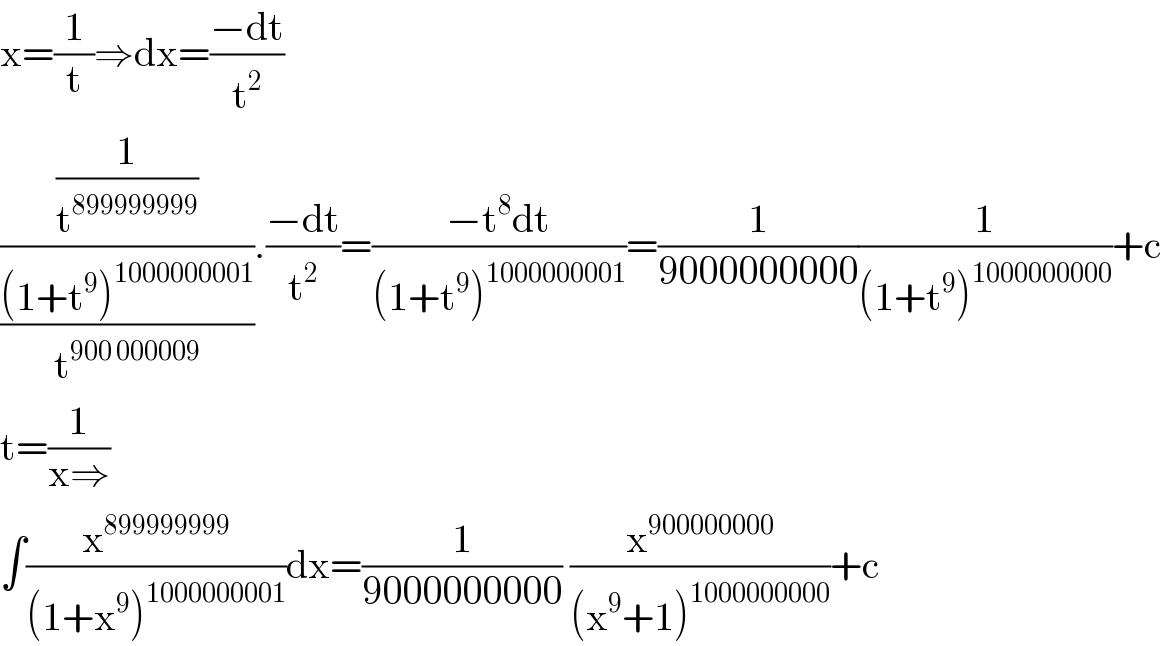
$$\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}\Rightarrow\mathrm{dx}=\frac{−\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} } \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{899999999}} }}{\frac{\left(\mathrm{1}+\mathrm{t}^{\mathrm{9}} \right)^{\mathrm{1000000001}} }{\mathrm{t}^{\mathrm{900}\:\mathrm{000009}} }}.\frac{−\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }=\frac{−\mathrm{t}^{\mathrm{8}} \mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{9}} \right)^{\mathrm{1000000001}} }=\frac{\mathrm{1}}{\mathrm{9000000000}}\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{9}} \right)^{\mathrm{1000000000}} }+\mathrm{c} \\ $$$$\mathrm{t}=\frac{\mathrm{1}}{\mathrm{x}\Rightarrow} \\ $$$$\int\frac{\mathrm{x}^{\mathrm{899999999}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{9}} \right)^{\mathrm{1000000001}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{9000000000}}\:\frac{\mathrm{x}^{\mathrm{900000000}} }{\left(\mathrm{x}^{\mathrm{9}} +\mathrm{1}\right)^{\mathrm{1000000000}} }+\mathrm{c} \\ $$
